[next] [prev] [prev-tail] [tail] [up]

5 Polar geometry: energy orthogonality

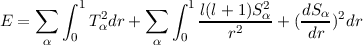
In a full sphere geometry, the energy of a vector field over the unit sphere, written in toroidal-poloidal form and then decomposed into spherical harmonics, may be defined as the sum

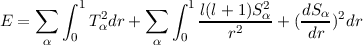
∑ ∫ 1 ∑ ∫ 1 2 E = T2αdr + l(l +-1)Sα-+ (dS-α)2dr α 0 α 0 r2 dr

where α indexes the spherical harmonics.

Auto-orthogonality can be extended to the case for which the basis functions are
(i) regular at the origin
(ii) satisfy relevant boundary conditions at r = 1 and are
(iii) orthogonal with respect to the inner product defined for the toroidal or poloidal scalars respectively

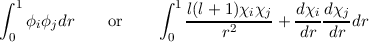
∫ 1 ∫ 1 l(l + 1)χiχj dχi dχj ϕiϕjdr or ----r2-----+ -dr-dr-dr 0 0

5.1 Toroidal, unconstrained

The toroidal component of a regular vector field that satisfies no particular boundary condition has an orthogonal basis of the form

(0,l+1∕2) Ψn = r(l+1)Pn-1 (2r2 - 1 ).

5.2 Toroidal, T(1) = 0

The toroidal component of a flow subject to nonslip boundary conditions, or the toroidal component of field in contact with an external electrical insulator simply satisfies regularity, T(1) = 0; an orthogonal basis is of the form

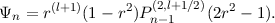
(l+1) 2 (2,l+1∕2) 2 Ψn = r (1- r)P n-1 (2r - 1).

5.3 Poloidal, unconstrained

An alternative to the Worland polynomials [4] (which are orthogonal in a different norm) is the orthogonal basis set

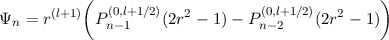
( ) (l+1) (0,l+1 ∕2) 2 (0,l+1∕2) 2 Ψn = r P n-1 (2r - 1) - Pn-2 (2r - 1)

for n ≥ 2.

The basis functions asymptotically collapse to a single family of one-sided Jacobi polynomials:

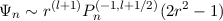
Ψn ~ r(l+1)P (n-1,l+1∕2)(2r2 - 1)

as n →∞.

5.4 Poloidal, S′(1) + lS(1) = 0

The poloidal component of a magnetic field in contact with an external electrical insulator satisfies regularity and (ii) S′(1) + lS(1) = 0 l ≥ 1 is the spherical harmonic degree. It has an orthogonal basis of the form

(l+1)( (0,l+1∕2) 2 (0,l+1∕2) 2 ) Ψn = r c0P n (2r - 1)+ c1P n-1 (2r - 1)+ c2

where

c0 = -2n2(l + 1) - n(l + 1)(2l - 1) - l(2l + 1)
c1 = 2(l + 1)n2 + (2l + 3)(l + 1)n + (2l + 1)2
c2 = 4nl + l(2l + 1)

Distinct from most other closed form expressions for the basis functions given in [2; 3], this has a constant term, although scaling only linearly in n, compared to the Jacobi polynomial coefficients that scale quadratically. Note that the coefficients are in the ratio (1,-1,0) in the limit of large n, so that the basis functions asymptotically collapse to a single family of one-sided Jacobi polynomials:

Ψn ~ r(l+1)P (n-1,l+1∕2)(2r2 - 1)

as n →∞. The figures below show some example basis functions and the asymptotic description of the 11th basis function.

PIC

Figure 6: The first 4 basis functions with l = 3.

PIC

Figure 7: The 11th basis function plotted with r(l+1)P11(-1,l+1∕2)(2r2 - 1) with l = 5.

5.5 Poloidal, S(1) = S′(1) = 0

The poloidal component of a nonslip flow satisfies regularity and S(1) = S′(1) = 0. Although an orthogonal basis can be written

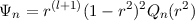
Ψn = r(l+1)(1- r2)2Qn (r2)

for some polynomial Qn, this has no [obvious] terse representation in terms of Jacobi polynomials. Instead, it may be written

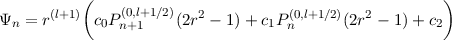
( ) (l+1) (0,l+1∕2) 2 (0,l+1∕2) 2 Ψn = r c0P n+1 (2r - 1)+ c1P n (2r - 1)+ c2

where

c0 = 2n2 + (2l + 3)n
c1 = -2n2 + (-7 - 2l)n - 2l - 5
c2 = 2l + 4n + 5
The coefficients are in the ratio (1,-1,0) in the limit of large n, so that the basis functions asymptotically collapse to a single family of one-sided Jacobi polynomials:
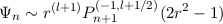
(-1,l+1∕2) Ψn ~ r(l+1)P n+1 (2r2 - 1)

as n →∞.

PIC

Figure 8: The first 4 basis functions for l = 3.

5.6 Poloidal, S(1) = 0

A poloidal component of a flow satisfying a non-penetration condition at r = 1 satisfies S(1) = 0 and has an orthogonal basis of the form

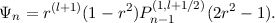
(1,l+1∕2) Ψn = r(l+1)(1- r2)P n-1 (2r2 - 1).

PIC

Figure 9: The first 4 basis functions for l = 3.

5.7 Poloidal, S′(1) = 0

The poloidal component of a magnetic field which describes a purely radial field satisfies S′(1) = 0, and has an orthogonal basis of the form

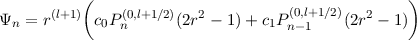
( ) Ψn = r(l+1) c0P (n0,l+1 ∕2)(2r2 - 1) + c1P (n0,-l+11∕2)(2r2 - 1)

where

c0 = -(2n - 1)(n + l)
c1 = (2n + 1)(n + l + 1)

Note that the coefficients are in the ratio (1,-1) in the limit of large n, so that the basis functions asymptotically collapse to a single family of one-sided Jacobi polynomials:

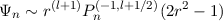
Ψn ~ r(l+1)P (n-1,l+1∕2)(2r2 - 1)

as n →∞.

5.8 Poloidal, all-space energy, S′(1) + lS(1) = 0

In an electrical insulator defined in the region r > 1 an interior magnetic field may be extended as:

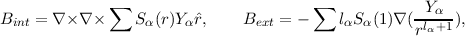
∑ ∑ -Yα-- Bint = ∇ × ∇ × Sα(r)Yαˆr, Bext = - lαSα (1)∇ (rlα+1),

where the boundary condition

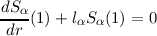
dS ---α(1)+ lαSα (1) = 0 dr

is satisfied. Noting that

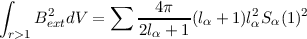
∫ ∑ B2extdV = --4π---(lα + 1)l2αS α(1)2 r>1 2lα + 1

it follows that the total energy over all space of the poloidal magnetic field may be defined as the sum

[ ∫ ] ∑ 4πlα(lα +-1) 1l(l +-1)S2α dS-α 2 2 E = 2lα + 1 r2 + ( dr ) dr + lαSα(1) α 0

where α indexes the harmonics.

An orthogonal basis that satisfies the orthogonality

∫ 1[l(l + 1)Ψn (r)Ψm (r) dΨn dΨm ] ---------2--------+ ---------dr + lΨn (1)Ψm (1) = δnm 0 r dr dr

and the boundary condition S′(1) + lS(1) = 0 is of the form

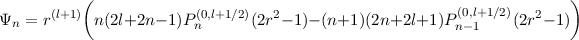
(l+1 )( (0,l+1∕2) 2 (0,l+1∕2) 2 ) Ψn = r n(2l+2n- 1)Pn (2r - 1)- (n+1 )(2n+2l+1 )Pn-1 (2r - 1 )

Note that the coefficients are in the ratio (1,-1) in the limit of large n, so that the basis functions asymptotically collapse to a single family of one-sided Jacobi polynomials:

(l+1) (-1,l+1∕2) 2 Ψn ~ r P n (2r - 1)

as n →∞. The figure shows some example basis functions normalised under the radial norm as defined above with l = 3.

PIC

Figure 10: The first 4 basis functions for l = 3.

[next] [prev] [prev-tail] [front] [up]