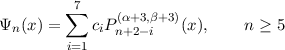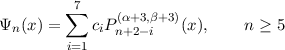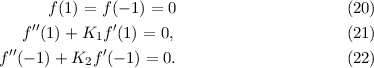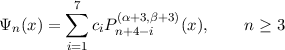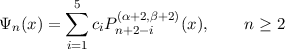3 Two sided, Cartesian
3.1 f(-1) = 0,f′′(1) + K1f′(1) + K2f(1) = 0
In the Cartesian domain [-1,1], we provide an orthogonal basis that satisfies the
generalised boundary conditions
| f(-1) | = 0 | |
|
| f′′(1) + K1f′(1) + K2f(1) | = 0. | | |
An unnormalised basis set may be written
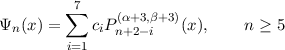
for any α > -1, β > -1. The functions Ψ1 and Ψ2 are given explicitly below.
The 7 coefficients ci are determined up to an arbitrary normalisation by
imposing
- Orthogonality to Ψ1, Ψ2, Ψ3, Ψ4 and
- Two boundary conditions
A generalised set ci for arbitrary {α,β} is currently beyond reach, but we
provide three cases with α = β = -1∕2, α = β = 1∕2 and α = β = 0
below.
Case(i) α = β = -1∕2
The ‘starting’ functions are given by
| Ψ1 | = 16K2 + 24K1 + 16 + 16xK1 + 16x - 16K2x2 - 8K
1x2 | |
|
| Ψ2 | = 400 - 368x + 576K1 + 64K2 - 272xK2 - 340xK12 - 48xK
22 - 232K
12x2 + 448K
1x3 + 48K
22x3 + 128K
2x3 + 268K
12x3 + 176K
2K1x3 - 80K
2K1x2 - 224xK
2K1 - 576x2 + 32K
2K1 + 160K12 - 744xK
1 - 872K1x2 - 208K
2x2 + 192x3 | |
|
| Ψ3 | = 19840 + 86080x + 17320K1 + 2000K2 + 3680K2K1x4 + 3280xK
2 + 6120xK12 - 16700K
12x2 - 560K
22x2 - 58480K
1x3 - 5600K
2x3 - 7280K
12x3 - 1120K
2K1x3 - 4880K
2K1x2 + 720xK
2K1 - 100800x2 + 80K
22 + 66880x4 + 800K
2K1 + 3260K12 + 48680xK
1 - 82480K1x2 - 11360K
2x2 + 12280K
12x4 + 55360K
1x4 + 7040K
2x4 + 480K
22x4 - 100160x3 | |
|
| Ψ4 | = 634640 - 2464240x + 175680K1 + 6720K2 - 41600K2K1x5 + 9600K
2K1x4 - 75920xK
2 - 118580xK12 - 1200xK
22 - 110760K
12x2 + 3205760K
1x3 + 4400K
22x3 + 240640K
2x3 + 366860K
12x3 - 4458240x5 - 1985280K
1x5 - 238880K
12x5 - 145920K
2x5 - 3200K
22x5 + 62000K
2K1x3 - 8400K
2K1x2 - 18400xK
2K1 - 4927680x2 + 4624640x4 + 800K
2K1 + 11680K12 - 1088680xK
1 - 1534760K1x2 - 66640K
2x2 + 108480K
12x4 + 1490880K
1x4 + 78720K
2x4 + 7254080x3 | | |
| c[1] | = 64(n - 1)(n + 5)(n + 4)n2(n + 6)(n + 1)(-72 - 1332n + 216K
1 + 3024K2 + 560n7 - 3024nK
12 - 216n2K
1 - 3024n2K
2 + 4536n3K
12 - 756n2K
12 + 7560nK
2K1 + 7560n2K
2K1 + 3996nK1 - 4536nK2 - 7344n3K
1 + 3024n3K
2 + 2268n4K
12 + 3240n5K
1 - 972n4K
1 + 1512n4K
2 + 1080n6K
1 + 632n2 + 3008n3 - 656n4 - 2200n5 - 80n6 + 140n8 + 11340K
22 - 3780K
2K1 - 189K12) | |
|
| c[2] | = -128(2n + 7)(2n + 1)(n + 3)(140n6 + 420n5 + 810n4K
1 - 130n4 + 1620n3K
1 - 960n3 - 756n2K
1 - 28n2 + 1134n2K
12 + 756n2K
2 + 1134nK12 + 756nK
2 + 522n - 1566nK1 + 1890K2K1 + 837K1 - 1323K12 + 36 + 378K
2)(n - 1)(n + 5)(n + 4)n2 | |
|
| c[3] | = -16(2n + 5)(n + 2)(2n + 7)(-648n - 9160n7 + 54999nK
12 + 26892n2K
1 + 104328n2K
2 - 756n3K
12 - 42903n2K
12 + 56700nK
2K1 + 117180n2K
2K1 - 20736nK1 - 18144nK2 + 65124n3K
1 + 34776n3K
2 + 61236n4K
12 + 75600n3K
2K1 - 13500n5K
1 + 22680n5K
2 - 31104n4K
1 + 33264n4K
2 + 34020n5K
12 + 39204n6K
1 + 21600n7K
1 + 56700nK22 + 22680n4K
2K1 + 34020n2K
22 + 6804n6K
12 + 4536n6K
2 + 3240n8K
1 - 11484n2 - 46908n3 + 39208n4 + 38240n5 - 19928n6 + 6760n8 + 3500n9 + 420n10 + 68040K
22 + 68040K
2K1 + 17010K12)(n - 1)(n + 4) | |
|
| c[4] | = 128(2n + 5)(2n + 3)(n + 3)(2n + 7)(18n + 2835K1 + 5670K2 + 1120n7 + 12096nK
12 + 3834n2K
1 + 756n2K
2 + 4536n3K
12 + 10584n2K
12 + 3780nK
2K1 + 1890n2K
2K1 + 9396nK1 - 4536nK2 + 5616n3K
1 + 3024n3K
2 + 1134n4K
12 + 4860n5K
1 + 9504n4K
1 + 756n4K
2 + 810n6K
1 + 7857n2 + 1768n3 - 4918n4 - 80n5 + 2600n6 + 140n8 + 5670K
2K1 + 2835K12)(n + 1)(n - 1) | |
|
| c[5] | = 4(2n + 5)(2n + 3)(2n + 1)(2n + 7)(-792n + 136080K1 + 272160K2 + 16520n7 + 326781nK
12 + 669492n2K
1 - 31752n2K
2 + 218484n3K
12 + 342657n2K
12 + 230580nK
2K1 + 207900n2K
2K1 + 599616nK1 + 139104nK2 + 208764n3K
1 + 49896n3K
2 + 129276n4K
12 + 105840n3K
2K1 + 121068n5K
1 + 31752n5K
2 + 36936n4K
1 + 78624n4K
2 + 47628n5K
12 + 99684n6K
1 + 30240n7K
1 + 79380nK22 + 22680n4K
2K1 + 34020n2K
22 + 6804n6K
12 + 4536n6K
2 + 3240n8K
1 + 348876n2 + 521212n3 + 129928n4 - 148576n5 - 75368n6 + 19360n8 + 4900n9 + 420n10 + 90720K
22 + 181440K
2K1 + 68040K12)n | |
|
| c[6] | = -8(2n + 7)(2n + 5)(2n + 1)(2n - 1)(n + 2)(2n + 3)2(140n6 + 1260n5 + 810n4K
1 + 4070n4 + 4860n3K
1 + 5520n3 + 2612n2 + 1134n2K
12 + 8964n2K
1 + 756n2K
2 + 6n + 5022nK1 + 3402nK12 + 2268nK
2 + 945K1 + 1890K2K1 + 945K12 + 1890K
2)(n - 1) | |
|
| c[7] | = -(2n + 7)(2n + 5)(2n + 3)(2n + 1)(2n - 1)(2n - 3)(n + 2)(-108n + 1680n7 + 18144nK
12 + 20520n2K
1 + 15120n2K
2 + 13608n3K
12 + 26460n2K
12 + 22680nK
2K1 + 7560n2K
2K1 + 324nK1 + 4536nK2 + 42768n3K
1 + 9072n3K
2 + 2268n4K
12 + 9720n5K
1 + 31428n4K
1 + 1512n4K
2 + 1080n6K
1 - 1800n2 + 4224n3 + 16544n4 + 16920n5 + 7760n6 + 140n8 + 11340K
22 + 11340K
2K1 + 2835K12) | | |
Expressions for all quantities involved are provided below.
Psi_1:=16*K_2+24*K_1+16+16*x*K_1+16*x-16*K_2*x^2-8*K_1*x^2;
Psi_2:=400-368*x+576*K_1+64*K_2-224*x*K_2*K_1-80*K_2*K_1*x^2+176*K_2*K_1*x^3-872*K_1*x^2-208*K_2*x^2+192*x^3-48*x*K_2^2-232*K_1^2*x^2-272*x*K_2-340*x*K_1^2+268*K_1^2*x^3+448*K_1*x^3+48*K_2^2*x^3+128*K_2*x^3+32*K_2*K_1+160*K_1^2-576*x^2-744*x*K_1;
Psi_3:=19840+86080*x+17320*K_1+2000*K_2+720*x*K_2*K_1-4880*K_2*K_1*x^2-1120*K_2*K_1*x^3+3680*K_2*K_1*x^4-82480*K_1*x^2-11360*K_2*x^2-100160*x^3-16700*K_1^2*x^2+3280*x*K_2+6120*x*K_1^2-560*K_2^2*x^2-7280*K_1^2*x^3-58480*K_1*x^3-5600*K_2*x^3+66880*x^4+80*K_2^2+12280*K_1^2*x^4+55360*K_1*x^4+7040*K_2*x^4+480*K_2^2*x^4+800*K_2*K_1+3260*K_1^2-100800*x^2+48680*x*K_1;
Psi_4:=634640-2464240*x+175680*K_1+6720*K_2-18400*x*K_2*K_1-8400*K_2*K_1*x^2+62000*K_2*K_1*x^3+9600*K_2*K_1*x^4-41600*K_2*K_1*x^5-1534760*K_1*x^2-66640*K_2*x^2-238880*K_1^2*x^5+7254080*x^3-1985280*K_1*x^5-145920*K_2*x^5-3200*K_2^2*x^5-1200*x*K_2^2-110760*K_1^2*x^2-75920*x*K_2-118580*x*K_1^2+366860*K_1^2*x^3+3205760*K_1*x^3+4400*K_2^2*x^3+240640*K_2*x^3+4624640*x^4+108480*K_1^2*x^4+1490880*K_1*x^4+78720*K_2*x^4+800*K_2*K_1+11680*K_1^2-4927680*x^2-1088680*x*K_1-4458240*x^5;
c[1]:=64*(n-1)*(n+5)*(n+4)*n^2*(n+6)*(n+1)*(-72-1332*n+216*K_1+3024*K_2+560*n^7-3024*n*K_1^2-216*n^2*K_1-3024*n^2*K_2+4536*n^3*K_1^2-756*n^2*K_1^2+7560*n*K_2*K_1+7560*n^2*K_2*K_1+3996*n*K_1-4536*n*K_2-7344*n^3*K_1+3024*n^3*K_2+2268*n^4*K_1^2+3240*n^5*K_1-972*n^4*K_1+1512*n^4*K_2+1080*n^6*K_1+632*n^2+3008*n^3-656*n^4-2200*n^5-80*n^6+140*n^8+11340*K_2^2-3780*K_2*K_1-189*K_1^2);
c[2]:=-128*(2*n+7)*(2*n+1)*(n+3)*(140*n^6+420*n^5+810*n^4*K_1-130*n^4+1620*n^3*K_1-960*n^3-756*n^2*K_1-28*n^2+1134*n^2*K_1^2+756*n^2*K_2+1134*n*K_1^2+756*n*K_2+522*n-1566*n*K_1+1890*K_2*K_1+837*K_1-1323*K_1^2+36+378*K_2)*(n-1)*(n+5)*(n+4)*n^2;
c[3]:=-16*(2*n+5)*(n+2)*(2*n+7)*(-648*n-9160*n^7+54999*n*K_1^2+26892*n^2*K_1+104328*n^2*K_2-756*n^3*K_1^2-42903*n^2*K_1^2+56700*n*K_2*K_1+117180*n^2*K_2*K_1-20736*n*K_1-18144*n*K_2+65124*n^3*K_1+34776*n^3*K_2+61236*n^4*K_1^2+75600*n^3*K_2*K_1-13500*n^5*K_1+22680*n^5*K_2-31104*n^4*K_1+33264*n^4*K_2+34020*n^5*K_1^2+39204*n^6*K_1+21600*n^7*K_1+56700*n*K_2^2+22680*n^4*K_2*K_1+34020*n^2*K_2^2+6804*n^6*K_1^2+4536*n^6*K_2+3240*n^8*K_1-11484*n^2-46908*n^3+39208*n^4+38240*n^5-19928*n^6+6760*n^8+3500*n^9+420*n^10+68040*K_2^2+68040*K_2*K_1+17010*K_1^2)*(n-1)*(n+4);
c[4]:=128*(2*n+5)*(2*n+3)*(n+3)*(2*n+7)*(18*n+2835*K_1+5670*K_2+1120*n^7+12096*n*K_1^2+3834*n^2*K_1+756*n^2*K_2+4536*n^3*K_1^2+10584*n^2*K_1^2+3780*n*K_2*K_1+1890*n^2*K_2*K_1+9396*n*K_1-4536*n*K_2+5616*n^3*K_1+3024*n^3*K_2+1134*n^4*K_1^2+4860*n^5*K_1+9504*n^4*K_1+756*n^4*K_2+810*n^6*K_1+7857*n^2+1768*n^3-4918*n^4-80*n^5+2600*n^6+140*n^8+5670*K_2*K_1+2835*K_1^2)*(n+1)*(n-1);
c[5]:=4*(2*n+5)*(2*n+3)*(2*n+1)*(2*n+7)*(-792*n+136080*K_1+272160*K_2+16520*n^7+326781*n*K_1^2+669492*n^2*K_1-31752*n^2*K_2+218484*n^3*K_1^2+342657*n^2*K_1^2+230580*n*K_2*K_1+207900*n^2*K_2*K_1+599616*n*K_1+139104*n*K_2+208764*n^3*K_1+49896*n^3*K_2+129276*n^4*K_1^2+105840*n^3*K_2*K_1+121068*n^5*K_1+31752*n^5*K_2+36936*n^4*K_1+78624*n^4*K_2+47628*n^5*K_1^2+99684*n^6*K_1+30240*n^7*K_1+79380*n*K_2^2+22680*n^4*K_2*K_1+34020*n^2*K_2^2+6804*n^6*K_1^2+4536*n^6*K_2+3240*n^8*K_1+348876*n^2+521212*n^3+129928*n^4-148576*n^5-75368*n^6+19360*n^8+4900*n^9+420*n^10+90720*K_2^2+181440*K_2*K_1+68040*K_1^2)*n;
c[6]:=-8*(2*n+7)*(2*n+5)*(2*n+1)*(2*n-1)*(n+2)*(2*n+3)^2*(140*n^6+1260*n^5+810*n^4*K_1+4070*n^4+4860*n^3*K_1+5520*n^3+2612*n^2+1134*n^2*K_1^2+8964*n^2*K_1+756*n^2*K_2+6*n+5022*n*K_1+3402*n*K_1^2+2268*n*K_2+945*K_1+1890*K_2*K_1+945*K_1^2+1890*K_2)*(n-1);
c[7]:=-(2*n+7)*(2*n+5)*(2*n+3)*(2*n+1)*(2*n-1)*(2*n-3)*(n+2)*(-108*n+1680*n^7+18144*n*K_1^2+20520*n^2*K_1+15120*n^2*K_2+13608*n^3*K_1^2+26460*n^2*K_1^2+22680*n*K_2*K_1+7560*n^2*K_2*K_1+324*n*K_1+4536*n*K_2+42768*n^3*K_1+9072*n^3*K_2+2268*n^4*K_1^2+9720*n^5*K_1+31428*n^4*K_1+1512*n^4*K_2+1080*n^6*K_1-1800*n^2+4224*n^3+16544*n^4+16920*n^5+7760*n^6+140*n^8+11340*K_2^2+11340*K_2*K_1+2835*K_1^2);
Case(ii) α = β = 1∕2
The ‘starting’ functions are given by
| Ψ1 | = 20K2 + 30K1 + 20 + 20xK1 + 20x - 20K2x2 - 10K
1x2 | |
|
| Ψ2 | = 260 - 540x + 400K1 + 80K2 + 200x3 - 540xK
2 - 495xK12 - 100xK
22 - 270K
12x2 + 345K
12x3 + 520K
1x3 + 240K
2x3 + 100K
22x3 + 40K
2K1 + 120K12 - 600x2 - 1110xK
1 - 380K2x2 - 990K
1x2 + 340K
2K1x3 - 140K
2K1x2 - 440xK
2K1 | |
|
| Ψ3 | = 106240 + 405120x + 96500K1 + 20200K2 + 1000K22 - 609920x3 + 33000xK
2 + 35700xK12 - 143850K
12x2 - 9000K
22x2 - 55200K
12x3 - 407200K
1x3 - 72000K
2x3 + 8400K
2K1 + 19950K12 + 104400K
12x4 + 412800K
1x4 + 8000K
22x4 + 96000K
2x4 - 739200x2 + 256500xK
1 - 155200K2x2 - 660000K
1x2 + 428160x4 - 14400K
2K1x3 - 68200K
2K1x2 + 7400xK
2K1 + 52800K2K1x4 | |
|
| Ψ4 | = 489640 - 2922840x + 165600K1 + 12960K2 + 10298240x3 - 200280xK
2 - 185590xK12 - 4200xK
22 - 161740K
12x2 + 698990K
12x3 + 5330040K
1x3 + 765680K
2x3 + 18200K
22x3 + 1680K
2K1 + 13040K12 - 6154880x5 - 148400K
2K1x5 + 191400K
12x4 + 2303400K
1x4 + 242000K
2x4 - 470700K
12x5 - 3318400K
1x5 - 480000K
2x5 - 14000K
22x5 - 5253760x2 - 1483420xK
1 - 169560K2x2 - 1940780K
1x2 + 5984640x4 + 210280K
2K1x3 - 22680K
2K1x2 - 52080xK
2K1 + 30800K2K1x4 | | |
| c[1] | = 64(n + 8)(3600 - 73500n - 7920K1 + 142560K2 + 3024n7 - 83160nK
12 - 173800n2K
1 + 23760n2K
2 + 59400n3K
12 + 61380n2K
12 + 249480nK
2K1 + 83160n2K
2K1 + 161700nK1 - 249480nK2 - 68640n3K
1 + 71280n3K
2 + 9900n4K
12 + 27720n5K
1 + 57860n4K
1 + 11880n4K
2 + 3080n6K
1 + 115288n2 + 960n3 - 56288n4 - 3528n5 + 10192n6 + 252n8 + 207900K
22 - 124740K
2K1 + 4455K12)n2(n + 7)(n + 5)(n + 6)(n + 1)2 | |
|
| c[2] | = -384n2(n + 7)(n + 5)(n + 6)(n + 1)(2n + 9)(2n + 3)(n + 4)(84n6 + 756n5 + 770n4K
1 + 1582n4 + 4620n3K
1 - 1848n3 + 3740n2K
1 - 4724n2 + 1650n2K
12 + 1980n2K
2 + 4950nK12 + 5940nK
2 + 4350n - 9570nK1 + 6930K2K1 + 3905K1 - 3135K12 - 200 - 990K
2) | |
|
| c[3] | = -48(n + 3)(2n + 9)(2n + 7)(13200n + 110880K1 + 221760K2 + 86072n7 + 27885nK
12 - 302500n2K
1 + 1120680n2K
2 + 861300n3K
12 + 722535n2K
12 + 2453220nK
2K1 + 1621620n2K
2K1 - 38280nK1 - 87120nK2 + 152020n3K
1 + 922680n3K
2 + 424380n4K
12 + 554400n3K
2K1 + 559900n5K
1 + 122760n5K
2 + 630520n4K
1 + 459360n4K
2 + 102300n5K
12 + 227260n6K
1 + 43120n7K
1 + 623700nK22 + 83160n4K
2K1 + 207900n2K
22 + 9900n6K
12 + 11880n6K
2 + 3080n8K
1 - 33356n2 - 98668n3 - 80296n4 - 15856n5 + 94856n6 + 29344n8 + 4452n9 + 252n10 + 1663200K
22 + 554400K
2K1 - 138600K12)(n + 5)(n + 6)n | |
|
| c[4] | = 192n(n + 5)(2n + 9)(2n + 7)(2n + 5)(n + 4)(n + 2)(-600n - 31185K1 - 62370K2 + 2688n7 + 146520nK
12 + 62260n2K
1 + 57420n2K
2 + 26400n3K
12 + 89430n2K
12 + 55440nK
2K1 + 13860n2K
2K1 - 81840nK1 - 23760nK2 + 139920n3K
1 + 31680n3K
2 + 3300n4K
12 + 18480n5K
1 + 79090n4K
1 + 3960n4K
2 + 1540n6K
1 - 53878n2 - 60912n3 + 14114n4 + 36624n5 + 15596n6 + 168n8 + 103950K
2K1 + 51975K12) | |
|
| c[5] | = 12(n + 1)(2n + 9)(2n + 7)(2n + 5)(2n + 3)(n + 4)(18000n + 223944n7 + 2932875nK
12 - 1267860n2K
1 + 1199880n2K
2 + 2232780n3K
12 + 3671415n2K
12 + 5197500nK
2K1 + 2952180n2K
2K1 - 1287000nK1 - 1782000nK2 + 1509420n3K
1 + 1991880n3K
2 + 754380n4K
12 + 776160n3K
2K1 + 1444740n5K
1 + 162360n5K
2 + 2579720n4K
1 + 855360n4K
2 + 135300n5K
12 + 399740n6K
1 + 55440n7K
1 + 1039500nK22 + 83160n4K
2K1 + 207900n2K
22 + 9900n6K
12 + 11880n6K
2 + 3080n8K
1 - 368700n2 - 2056980n3 - 1609064n4 - 34512n5 + 444520n6 + 50512n8 + 5628n9 + 252n10 + 2494800K
22 + 2494800K
2K1 + 623700K12) | |
|
| c[6] | = -24n(2n + 9)(2n + 7)(2n + 3)(2n + 1)(n + 4)(n + 3)(2n + 5)2(84n6 + 1260n5 + 6622n4 + 770n4K
1 + 7700n3K
1 + 13720n3 + 8044n2 + 1650n2K
12 + 22220n2K
1 + 1980n2K
2 + 9900nK2 + 8250nK12 - 30n + 14850nK
1 + 3465K12 + 6930K
2K1 + 6930K2 + 3465K1) | |
|
| c[7] | = -(2n + 9)(2n + 7)(2n + 5)(2n + 3)(2n + 1)(2n - 1)(n + 4)(n + 3)(1500n + 5040n7 + 257400nK
12 + 290840n2K
1 + 308880n2K
2 + 99000n3K
12 + 298980n2K
12 + 415800nK
2K1 + 83160n2K
2K1 - 3300nK1 + 59400nK2 + 501600n3K
1 + 118800n3K
2 + 9900n4K
12 + 46200n5K
1 + 242660n4K
1 + 11880n4K
2 + 3080n6K
1 - 31400n2 + 64320n3 + 202432n4 + 135240n5 + 38416n6 + 252n8 + 207900K
22 + 207900K
2K1 + 51975K12) | | |
Expressions for all quantities involved are provided below.
Psi_1:=20*K_2+30*K_1+20+20*x*K_1+20*x-20*K_2*x^2-10*K_1*x^2;
Psi_2:=260-540*x+400*K_1+80*K_2+200*x^3-540*x*K_2-495*x*K_1^2-100*x*K_2^2-270*K_1^2*x^2+345*K_1^2*x^3+520*K_1*x^3+240*K_2*x^3+100*K_2^2*x^3+40*K_2*K_1+120*K_1^2-600*x^2-1110*x*K_1-380*K_2*x^2-990*K_1*x^2+340*K_2*K_1*x^3-140*K_2*K_1*x^2-440*x*K_2*K_1;
Psi_3:=106240+405120*x+96500*K_1+20200*K_2+1000*K_2^2-609920*x^3+33000*x*K_2+35700*x*K_1^2-143850*K_1^2*x^2-55200*K_1^2*x^3-407200*K_1*x^3-72000*K_2*x^3+8400*K_2*K_1+19950*K_1^2+104400*K_1^2*x^4+412800*K_1*x^4+96000*K_2*x^4+8000*K_2^2*x^4-739200*x^2+256500*x*K_1-155200*K_2*x^2-660000*K_1*x^2-9000*K_2^2*x^2+428160*x^4-14400*K_2*K_1*x^3-68200*K_2*K_1*x^2+7400*x*K_2*K_1+52800*K_2*K_1*x^4;
Psi_4:=489640-2922840*x+165600*K_1+12960*K_2+10298240*x^3-200280*x*K_2-185590*x*K_1^2-4200*x*K_2^2-161740*K_1^2*x^2+698990*K_1^2*x^3+5330040*K_1*x^3+765680*K_2*x^3+18200*K_2^2*x^3+1680*K_2*K_1+13040*K_1^2-6154880*x^5-148400*K_2*K_1*x^5+191400*K_1^2*x^4+2303400*K_1*x^4+242000*K_2*x^4-470700*K_1^2*x^5-3318400*K_1*x^5-480000*K_2*x^5-14000*K_2^2*x^5-5253760*x^2-1483420*x*K_1-169560*K_2*x^2-1940780*K_1*x^2+5984640*x^4+210280*K_2*K_1*x^3-22680*K_2*K_1*x^2-52080*x*K_2*K_1+30800*K_2*K_1*x^4;
c[1]:=64*(n+8)*(3600-73500*n-7920*K_1+142560*K_2+3024*n^7-83160*n*K_1^2-173800*n^2*K_1+23760*n^2*K_2+59400*n^3*K_1^2+61380*n^2*K_1^2+249480*n*K_2*K_1+83160*n^2*K_2*K_1+161700*n*K_1-249480*n*K_2-68640*n^3*K_1+71280*n^3*K_2+9900*n^4*K_1^2+27720*n^5*K_1+57860*n^4*K_1+11880*n^4*K_2+3080*n^6*K_1+115288*n^2+960*n^3-56288*n^4-3528*n^5+10192*n^6+252*n^8+207900*K_2^2-124740*K_2*K_1+4455*K_1^2)*n^2*(n+7)*(n+5)*(n+6)*(n+1)^2;
c[2]:=-384*n^2*(n+7)*(n+5)*(n+6)*(n+1)*(2*n+9)*(2*n+3)*(n+4)*(84*n^6+756*n^5+770*n^4*K_1+1582*n^4+4620*n^3*K_1-1848*n^3+3740*n^2*K_1-4724*n^2+1650*n^2*K_1^2+1980*n^2*K_2+4950*n*K_1^2+5940*n*K_2+4350*n-9570*n*K_1+6930*K_2*K_1+3905*K_1-3135*K_1^2-200-990*K_2);
c[3]:=-48*(n+3)*(2*n+9)*(2*n+7)*(13200*n+110880*K_1+221760*K_2+86072*n^7+27885*n*K_1^2-302500*n^2*K_1+1120680*n^2*K_2+861300*n^3*K_1^2+722535*n^2*K_1^2+2453220*n*K_2*K_1+1621620*n^2*K_2*K_1-38280*n*K_1-87120*n*K_2+152020*n^3*K_1+922680*n^3*K_2+424380*n^4*K_1^2+554400*n^3*K_2*K_1+559900*n^5*K_1+122760*n^5*K_2+630520*n^4*K_1+459360*n^4*K_2+102300*n^5*K_1^2+227260*n^6*K_1+43120*n^7*K_1+623700*n*K_2^2+83160*n^4*K_2*K_1+207900*n^2*K_2^2+9900*n^6*K_1^2+11880*n^6*K_2+3080*n^8*K_1-33356*n^2-98668*n^3-80296*n^4-15856*n^5+94856*n^6+29344*n^8+4452*n^9+252*n^10+1663200*K_2^2+554400*K_2*K_1-138600*K_1^2)*(n+5)*(n+6)*n;
c[4]:=192*n*(n+5)*(2*n+9)*(2*n+7)*(2*n+5)*(n+4)*(n+2)*(-600*n-31185*K_1-62370*K_2+2688*n^7+146520*n*K_1^2+62260*n^2*K_1+57420*n^2*K_2+26400*n^3*K_1^2+89430*n^2*K_1^2+55440*n*K_2*K_1+13860*n^2*K_2*K_1-81840*n*K_1-23760*n*K_2+139920*n^3*K_1+31680*n^3*K_2+3300*n^4*K_1^2+18480*n^5*K_1+79090*n^4*K_1+3960*n^4*K_2+1540*n^6*K_1-53878*n^2-60912*n^3+14114*n^4+36624*n^5+15596*n^6+168*n^8+103950*K_2*K_1+51975*K_1^2);
c[5]:=12*(n+1)*(2*n+9)*(2*n+7)*(2*n+5)*(2*n+3)*(n+4)*(18000*n+223944*n^7+2932875*n*K_1^2-1267860*n^2*K_1+1199880*n^2*K_2+2232780*n^3*K_1^2+3671415*n^2*K_1^2+5197500*n*K_2*K_1+2952180*n^2*K_2*K_1-1287000*n*K_1-1782000*n*K_2+1509420*n^3*K_1+1991880*n^3*K_2+754380*n^4*K_1^2+776160*n^3*K_2*K_1+1444740*n^5*K_1+162360*n^5*K_2+2579720*n^4*K_1+855360*n^4*K_2+135300*n^5*K_1^2+399740*n^6*K_1+55440*n^7*K_1+1039500*n*K_2^2+83160*n^4*K_2*K_1+207900*n^2*K_2^2+9900*n^6*K_1^2+11880*n^6*K_2+3080*n^8*K_1-368700*n^2-2056980*n^3-1609064*n^4-34512*n^5+444520*n^6+50512*n^8+5628*n^9+252*n^10+2494800*K_2^2+2494800*K_2*K_1+623700*K_1^2);
c[6]:=-24*n*(2*n+9)*(2*n+7)*(2*n+3)*(2*n+1)*(n+4)*(n+3)*(2*n+5)^2*(84*n^6+1260*n^5+6622*n^4+770*n^4*K_1+7700*n^3*K_1+13720*n^3+8044*n^2+1650*n^2*K_1^2+22220*n^2*K_1+1980*n^2*K_2+9900*n*K_2+8250*n*K_1^2-30*n+14850*n*K_1+3465*K_1^2+6930*K_2*K_1+6930*K_2+3465*K_1);
c[7]:=-(2*n+9)*(2*n+7)*(2*n+5)*(2*n+3)*(2*n+1)*(2*n-1)*(n+4)*(n+3)*(1500*n+5040*n^7+257400*n*K_1^2+290840*n^2*K_1+308880*n^2*K_2+99000*n^3*K_1^2+298980*n^2*K_1^2+415800*n*K_2*K_1+83160*n^2*K_2*K_1-3300*n*K_1+59400*n*K_2+501600*n^3*K_1+118800*n^3*K_2+9900*n^4*K_1^2+46200*n^5*K_1+242660*n^4*K_1+11880*n^4*K_2+3080*n^6*K_1-31400*n^2+64320*n^3+202432*n^4+135240*n^5+38416*n^6+252*n^8+207900*K_2^2+207900*K_2*K_1+51975*K_1^2);
Case(iii) α = β = 0
The ‘starting’ functions are given by
| Ψ1 | = 18K2 + 27K1 + 18 + 18xK1 + 18x - 18K2x2 - 9K
1x2 | |
|
| Ψ2 | = 144 - 216x + 216K1 + 36K2 - 162xK2K1 - 54K2K1x2 - 36xK
22 - 117K
12x2 + 144K
12x3 + 225K
1x3 + 126K
2K1x3 + 90K
2x3 + 36K
22x3 + 18K
2K1 + 63K12 - 270x2 - 441xK
1 - 144K2x2 - 432K
1x2 - 198xK
2 - 198xK12 + 90x3 | |
|
| Ψ3 | = 56133 + 224532x + 50094K1 + 8712K2 + 3168xK2K1 - 25344K2K1x2 - 61776K
12x2 - 3168K
22x2 - 24948K
12x3 - 189882K
1x3 - 5544K
2K1x3 - 27720K
2x3 + 396K
22 + 3564K
2K1 + 9999K12 + 19404K
2K1x4 + 205821x4 + 45045K
12x4 + 187110K
1x4 + 2772K
22x4 + 36036K
2x4 - 336798x2 + 136026xK
1 - 58212K2x2 - 291060K
1x2 + 14256xK
2 + 18216xK12 - 299376x3 | |
|
| Ψ4 | = 81774 - 403326x + 25542K1 + 1584K2 - 13662K2K1x5 - 5346xK
2K1 - 2376K2K1x2 - 20592K
12x2 + 78804K
12x3 + 633006K
1x3 - 396xK
22 + 19800K
2K1x3 + 74052K
2x3 + 1584K
22x3 - 52272K
12x5 - 45738K
2x5 - 1188K
22x5 - 392931K
1x5 - 785862x5 + 198K
2K1 + 1881K12 + 2970K
2K1x4 + 785862x4 + 22275K
12x4 + 282150K
1x4 + 23760K
2x4 - 756756x2 - 193743xK
1 - 18216K2x2 - 261360K
1x2 - 21186xK
2 - 22968xK12 + 1300068x3 | | |
| c[1] | = (n + 7)(-216n + 480K2 + 24n7 - 320nK
12 - 450n2K
1 - 80n2K
2 + 320n3K
12 + 160n2K
12 + 960nK
2K1 + 480n2K
2K1 + 540nK1 - 800nK2 - 480n3K
1 + 320n3K
2 + 80n4K
12 + 180n5K
1 + 180n4K
1 + 80n4K
2 + 30n6K
1 + 288n2 + 156n3 - 213n4 - 84n5 + 42n6 + 3n8 + 960K
22 - 480K
2K1)n(n + 6)(n + 1)(2n - 1)(n + 5)(2n + 1) | |
|
| c[2] | = -2n(n + 6)(n + 1)(2n - 1)(n + 5)(2n + 1)(n + 4)(2n + 7)(6n6 + 36n5 + 36n4 + 45n4K
1 + 180n3K
1 - 96n3 + 80n2K
12 + 45n2K
1 + 80n2K
2 - 90n2 + 160nK
2 + 160nK12 + 108n - 270nK
1 - 120K12 + 120K
1 + 240K2K1) | |
|
| c[3] | = -(2n + 5)(n + 4)(n + 3)(738n7 + 1680nK
12 + 2400n2K
1 + 10240n2K
2 + 7040n3K
12 + 2320n2K
12 + 17280nK
2K1 + 16320n2K
2K1 - 1680nK1 + 1440nK2 + 1260n3K
1 + 7280n3K
2 + 5600n4K
12 + 7200n3K
2K1 + 4770n5K
1 + 1840n5K
2 + 1800n4K
1 + 4880n4K
2 + 1840n5K
12 + 3390n6K
1 + 930n7K
1 + 6720nK22 + 1440n4K
2K1 + 2880n2K
22 + 240n6K
12 + 240n6K
2 + 90n8K
1 - 2160n2 - 468n3 + 1974n4 - 387n5 - 339n6 + 516n8 + 117n9 + 9n10 + 13440K
22 + 6720K
2K1)(2n - 1)(n + 5) | |
|
| c[4] | = 4(2n - 1)(2n + 7)(2n + 3)(n + 4)(n + 3)(n + 2)(72n7 + 1920nK
12 + 480n2K
1 + 520n2K
2 + 480n3K
12 + 1360n2K
12 + 720nK
2K1 + 240n2K
2K1 - 180nK1 - 600nK2 + 1575n3K
1 + 480n3K
2 + 80n4K
12 + 405n5K
1 + 1275n4K
1 + 80n4K
2 + 45n6K
1 + 108n2 - 657n3 - 231n4 + 405n5 + 297n6 + 6n8 + 1200K
2K1 + 600K12) | |
|
| c[5] | = (n + 1)(2n + 1)(n + 3)(n + 2)(2n + 7)(7200K1 + 14400K2 + 2898n7 + 31680nK
12 + 10500n2K
1 + 3040n2K
2 + 24160n3K
12 + 36160n2K
12 + 41760nK
2K1 + 29280n2K
2K1 + 16080nK1 - 4800nK2 + 9810n3K
1 + 15280n3K
2 + 10400n4K
12 + 10080n3K
2K1 + 16560n5K
1 + 2480n5K
2 + 19350n4K
1 + 9680n4K
2 + 2480n5K
12 + 6540n6K
1 + 1230n7K
1 + 10560nK22 + 1440n4K
2K1 + 2880n2K
22 + 240n6K
12 + 240n6K
2 + 90n8K
1 + 13392n2 + 2772n3 - 14172n4 - 7983n5 + 1929n6 + 1002n8 + 153n9 + 9n10 + 19200K
22 + 24000K
2K1 + 7200K12) | |
|
| c[6] | = -2n(n + 1)(2n - 1)(2n + 5)(n + 3)(2n + 7)(n + 2)2(6n6 + 72n5 + 306n4 + 45n4K
1 + 528n3 + 360n3K
1 + 288n2 + 855n2K
1 + 80n2K
12 + 80n2K
2 + 540nK1 + 320nK12 + 320nK
2 + 120K1 + 120K12 + 240K
2 + 240K2K1) | |
|
| c[7] | = -n(n + 1)(2n + 5)(n - 1)(n + 3)(n + 2)(2n + 7)(48n7 + 1280nK
12 + 1440n2K
1 + 1360n2K
2 + 640n3K
12 + 1600n2K
12 + 1920nK
2K1 + 480n2K
2K1 + 320nK2 + 2640n3K
1 + 640n3K
2 + 80n4K
12 + 360n5K
1 + 1530n4K
1 + 80n4K
2 + 30n6K
1 - 144n2 + 312n3 + 1047n4 + 840n5 + 294n6 + 3n8 + 960K
22 + 960K
2K1 + 240K12) | | |
Expressions for all quantities involved are provided below.
Psi_1:=18*K_2+27*K_1+18+18*x*K_1+18*x-18*K_2*x^2-9*K_1*x^2;
Psi_2:=144-216*x+216*K_1+36*K_2-162*x*K_2*K_1-54*K_2*K_1*x^2-117*K_1^2*x^2+144*K_1^2*x^3+225*K_1*x^3-36*x*K_2^2+126*K_2*K_1*x^3+90*K_2*x^3+36*K_2^2*x^3+18*K_2*K_1+63*K_1^2-270*x^2-441*x*K_1-144*K_2*x^2-432*K_1*x^2-198*x*K_2-198*x*K_1^2+90*x^3;
Psi_3:=56133+224532*x+50094*K_1+8712*K_2+3168*x*K_2*K_1-25344*K_2*K_1*x^2-61776*K_1^2*x^2-3168*K_2^2*x^2-24948*K_1^2*x^3-189882*K_1*x^3-5544*K_2*K_1*x^3-27720*K_2*x^3+396*K_2^2+3564*K_2*K_1+9999*K_1^2+19404*K_2*K_1*x^4+205821*x^4+45045*K_1^2*x^4+187110*K_1*x^4+2772*K_2^2*x^4+36036*K_2*x^4-336798*x^2+136026*x*K_1-58212*K_2*x^2-291060*K_1*x^2+14256*x*K_2+18216*x*K_1^2-299376*x^3;
Psi_4:=81774-403326*x+25542*K_1+1584*K_2-13662*K_2*K_1*x^5-5346*x*K_2*K_1-2376*K_2*K_1*x^2-20592*K_1^2*x^2+78804*K_1^2*x^3+633006*K_1*x^3-396*x*K_2^2+19800*K_2*K_1*x^3+74052*K_2*x^3+1584*K_2^2*x^3-52272*K_1^2*x^5-45738*K_2*x^5-1188*K_2^2*x^5-392931*K_1*x^5-785862*x^5+198*K_2*K_1+1881*K_1^2+2970*K_2*K_1*x^4+785862*x^4+22275*K_1^2*x^4+282150*K_1*x^4+23760*K_2*x^4-756756*x^2-193743*x*K_1-18216*K_2*x^2-261360*K_1*x^2-21186*x*K_2-22968*x*K_1^2+1300068*x^3;
c[1]:=(n+7)*(-216*n+480*K_2+24*n^7-320*n*K_1^2-450*n^2*K_1-80*n^2*K_2+320*n^3*K_1^2+160*n^2*K_1^2+960*n*K_2*K_1+480*n^2*K_2*K_1+540*n*K_1-800*n*K_2-480*n^3*K_1+320*n^3*K_2+80*n^4*K_1^2+180*n^5*K_1+180*n^4*K_1+80*n^4*K_2+30*n^6*K_1+288*n^2+156*n^3-213*n^4-84*n^5+42*n^6+3*n^8+960*K_2^2-480*K_2*K_1)*n*(n+6)*(n+1)*(2*n-1)*(n+5)*(2*n+1);
c[2]:=-2*n*(n+6)*(n+1)*(2*n-1)*(n+5)*(2*n+1)*(n+4)*(2*n+7)*(6*n^6+36*n^5+36*n^4+45*n^4*K_1+180*n^3*K_1-96*n^3+80*n^2*K_1^2+45*n^2*K_1+80*n^2*K_2-90*n^2+160*n*K_2+160*n*K_1^2+108*n-270*n*K_1-120*K_1^2+120*K_1+240*K_2*K_1);
c[3]:=-(2*n+5)*(n+4)*(n+3)*(738*n^7+1680*n*K_1^2+2400*n^2*K_1+10240*n^2*K_2+7040*n^3*K_1^2+2320*n^2*K_1^2+17280*n*K_2*K_1+16320*n^2*K_2*K_1-1680*n*K_1+1440*n*K_2+1260*n^3*K_1+7280*n^3*K_2+5600*n^4*K_1^2+7200*n^3*K_2*K_1+4770*n^5*K_1+1840*n^5*K_2+1800*n^4*K_1+4880*n^4*K_2+1840*n^5*K_1^2+3390*n^6*K_1+930*n^7*K_1+6720*n*K_2^2+1440*n^4*K_2*K_1+2880*n^2*K_2^2+240*n^6*K_1^2+240*n^6*K_2+90*n^8*K_1-2160*n^2-468*n^3+1974*n^4-387*n^5-339*n^6+516*n^8+117*n^9+9*n^10+13440*K_2^2+6720*K_2*K_1)*(2*n-1)*(n+5);
c[4]:=4*(2*n-1)*(2*n+7)*(2*n+3)*(n+4)*(n+3)*(n+2)*(72*n^7+1920*n*K_1^2+480*n^2*K_1+520*n^2*K_2+480*n^3*K_1^2+1360*n^2*K_1^2+720*n*K_2*K_1+240*n^2*K_2*K_1-180*n*K_1-600*n*K_2+1575*n^3*K_1+480*n^3*K_2+80*n^4*K_1^2+405*n^5*K_1+1275*n^4*K_1+80*n^4*K_2+45*n^6*K_1+108*n^2-657*n^3-231*n^4+405*n^5+297*n^6+6*n^8+1200*K_2*K_1+600*K_1^2);
c[5]:=(n+1)*(2*n+1)*(n+3)*(n+2)*(2*n+7)*(7200*K_1+14400*K_2+2898*n^7+31680*n*K_1^2+10500*n^2*K_1+3040*n^2*K_2+24160*n^3*K_1^2+36160*n^2*K_1^2+41760*n*K_2*K_1+29280*n^2*K_2*K_1+16080*n*K_1-4800*n*K_2+9810*n^3*K_1+15280*n^3*K_2+10400*n^4*K_1^2+10080*n^3*K_2*K_1+16560*n^5*K_1+2480*n^5*K_2+19350*n^4*K_1+9680*n^4*K_2+2480*n^5*K_1^2+6540*n^6*K_1+1230*n^7*K_1+10560*n*K_2^2+1440*n^4*K_2*K_1+2880*n^2*K_2^2+240*n^6*K_1^2+240*n^6*K_2+90*n^8*K_1+13392*n^2+2772*n^3-14172*n^4-7983*n^5+1929*n^6+1002*n^8+153*n^9+9*n^10+19200*K_2^2+24000*K_2*K_1+7200*K_1^2);
c[6]:=-2*n*(n+1)*(2*n-1)*(2*n+5)*(n+3)*(2*n+7)*(n+2)^2*(6*n^6+72*n^5+306*n^4+45*n^4*K_1+528*n^3+360*n^3*K_1+288*n^2+855*n^2*K_1+80*n^2*K_1^2+80*n^2*K_2+540*n*K_1+320*n*K_1^2+320*n*K_2+120*K_1+120*K_1^2+240*K_2+240*K_2*K_1);
c[7]:=-n*(n+1)*(2*n+5)*(n-1)*(n+3)*(n+2)*(2*n+7)*(48*n^7+1280*n*K_1^2+1440*n^2*K_1+1360*n^2*K_2+640*n^3*K_1^2+1600*n^2*K_1^2+1920*n*K_2*K_1+480*n^2*K_2*K_1+320*n*K_2+2640*n^3*K_1+640*n^3*K_2+80*n^4*K_1^2+360*n^5*K_1+1530*n^4*K_1+80*n^4*K_2+30*n^6*K_1-144*n^2+312*n^3+1047*n^4+840*n^5+294*n^6+3*n^8+960*K_2^2+960*K_2*K_1+240*K_1^2);
3.2 f(1) = f(-1) = 0,f′′(1) + K1f′(1) = f′′(-1) + K2f′(-1) = 0
In the Cartesian domain [-1,1], we provide a general formulation of
orthogonal basis functions that satisfy the generalised boundary conditions
An unnormalised basis set may be written
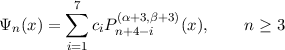
for any α > -1, β > -1. The functions Ψ1 and Ψ2 are given explicitly below.
The 7 coefficients ci are determined up to an arbitrary normalisation by
imposing
- Orthogonality to Ψ1, Ψ2 and
- Four boundary conditions
A generalised set ci for arbitrary {α,β} is currently beyond reach, but we
provide three cases with α = β = -1∕2, α = β = 1∕2 and α = β = 0
below.
Case(i) α = β = -1∕2
The ‘starting’ functions are given by
| Ψ1 | = -320K1 + 320K2 - 240x4 + 160xK
2 + 160xK1 + 480K1x2 + 80K
1K2 - 160K1K2x2 - 160K
2x3 - 160K
1x3 - 160K
1x4 + 160K
2x4 - 480K
2x2 - 1200 + 80K
1K2x4 + 1440x2 | |
|
| Ψ2 | = 26800K1K22x3 + 14800xK
12K
2 - 943320x - 27680K1 - 27680K2 - 4400K12K
2x2 - 249600K
1K2x3 + 153200xK
1K2 - 14800xK1K22 - 1400xK
12K
22 + 1347600x3 - 12000K
1K22x5 - 26800K
12K
2x3 + 2800K
12K
22x3 + 388400xK
2 - 388400xK1 + 87120K1x2 - 1400K
12K
22x5 + 96400K
1K2x5 + 12000K
12K
2x5 + 4960K
22 + 800K
1K22 + 3600K
12K
2x4 + 3600K
1K22x4 - 593360K
2x3 + 593360K
1x3 - 59440K
1x4 - 59440K
2x4 + 87120K
2x2 - 4400K
1K22x2 - 4960K
12 - 404280x5 - 38560xK
12 - 21120K
22x2 + 21120K
12x2 - 38560xK
22 + 65920K
22x3 + 65920K
12x3 + 16160K
22x4 - 16160K
12x4 - 204960K
1x5 + 204960K
2x5 - 27360K
22x5 - 27360K
12x5 + 800K
12K
2 | | |
| c[1] | = 64(n + 8)(n + 3)(61425 + 45720n + 18900K1 - 18900K2 + 15680n7 - 81040n3 + 467896n4 - 123456n2 + 117376n6 - 28350K
1K2 - 18900K22 + 56700K
1K22 + 99225K
12K
22 - 18900K
12 + 388640n5 - 56700K
12K
2 - 283500nK12K
2 + 95940n2K
1 - 60300nK1 + 81900nK22 + 81900nK
12 + 236880n2K
12 + 60300nK
2 - 673200n3K
2 + 8820n4K
12 + 56700n2K
1K22 + 283500nK
1K22 - 56700n2K
12K
2 + 236880n2K
22 - 95940n2K
2 + 88200n3K
12 + 673200n3K
1 + 88200n3K
22 + 75600n5K
1 + 382320n4K
1 + 8820n4K
22 - 382320n4K
2 - 75600n5K
2 - 5040n6K
2 + 5040n6K
1 - 162000nK1K2 - 842400n2K
1K2 - 324000n3K
1K2 - 32400n4K
1K2 + 784n8)(n + 7)(n + 2)2n(n + 1)2 | |
|
| c[2] | = -40320(n + 7)(n + 2)2n(n + 1)2(2n + 11)(2n + 5)(n + 5)(K
2 + K1)(-14n2K
1 - 70nK1 + 45K1K2 - 6K1 - 4n4 - 40n3 - 96n2 + 20n - 15 + 14n2K
2 + 70nK2 + 6K2) | |
|
| c[3] | = -16(n + 1)2n(n + 4)(2n + 11)(2n + 9)(-1256850 + 1955835n + 4498200K
1 - 4498200K2 + 7225120n7 + 88252280n3 + 115141760n4 + 31313067n2 + 30973256n6 - 22623300K
1K2 + 3439800K22 + 13494600K
1K22 + 26460n6K
22 + 7739550K
12K
22 + 26460n6K
12 + 3439800K
12 + 78963160n5 - 13494600K
12K
2 - 27726300nK12K
2 + 91714680n2K
1 + 33484500nK1 + 19246500nK22 + 19246500nK
12 + 28035000n2K
12 - 33484500nK
2 - 115006320n3K
2 + 4238640n4K
12 + 2494800n3K
1K22 + 13267800n2K
1K22 + 27726300nK
1K22 - 13267800n2K
12K
2 + 28035000n2K
22 - 91714680n2K
2 + 538020n5K
12 + 15917580n3K
12 + 115006320n3K
1 + 15917580n3K
22 - 2494800n3K
12K
2 + 23124960n5K
1 + 70508700n4K
1 + 4238640n4K
22 - 70508700n4K
2 + 538020n5K
22 - 23124960n5K
2 - 4176000n6K
2 + 4176000n6K
1 + 393120n7K
1 - 393120n7K
2 + 2679075nK12K
22 - 80825850nK
1K2 + 297675n2K
12K
22 - 111022650n2K
1K2 - 60620400n3K
1K2 - 170100n4K
12K
2 + 170100n4K
1K22 - 15746400n4K
1K2 - 1976400n5K
1K2 - 97200n6K
1K2 + 15120n8K
1 - 15120n8K
2 + 74480n9 + 2352n10 + 993440n8) | |
|
| c[4] | = 20160(n + 5)(2n + 11)(2n + 9)(2n + 7)(K2 + K1)(-28n4K
1 - 336n3K
1 - 1132n2K
1 + 90n2K
1K2 - 744nK1 + 540nK1K2 + 315K1K2 + 350K1 - 8n6 - 144n5 - 900n4 - 2160n3 - 1122n2 + 1044n + 455 + 28n4K
2 + 336n3K
2 + 1132n2K
2 + 744nK2 - 350K2)(n + 1)n(n + 3) | |
|
| c[5] | = 4(n + 2)(2n + 11)(2n + 9)(2n + 7)(2n + 5)(n + 5)(2381400 + 9770985n + 6350400K1 - 6350400K2 + 4897760n7 + 35114440n3 + 45389840n4 + 21852987n2 + 17660936n6 - 14288400K
1K2 + 3175200K22 + 6350400K
1K22 + 26460n6K
22 + 2381400K
12K
22 + 26460n6K
12 + 3175200K
12 + 37113800n5 - 6350400K
12K
2 - 9015300nK12K
2 + 40367160n2K
1 + 22852620nK1 + 8407980nK22 + 8407980nK
12 + 9324000n2K
12 - 22852620nK
2 - 44708400n3K
2 + 2386440n4K
12 + 1587600n3K
1K22 + 5103000n2K
1K22 + 9015300nK
1K22 - 5103000n2K
12K
2 + 9324000n2K
22 - 40367160n2K
2 + 414540n5K
12 + 6429780n3K
12 + 44708400n3K
1 + 6429780n3K
22 - 1587600n3K
12K
2 + 12903840n5K
1 + 31499100n4K
1 + 2386440n4K
22 - 31499100n4K
2 + 414540n5K
22 - 12903840n5K
2 - 2905920n6K
2 + 2905920n6K
1 + 332640n7K
1 - 332640n7K
2 + 893025nK12K
22 - 37223550nK
1K2 + 297675n2K
12K
22 - 41621850n2K
1K2 - 25693200n3K
1K2 - 170100n4K
12K
2 + 170100n4K
1K22 - 8942400n4K
1K2 - 1522800n5K
1K2 - 97200n6K
1K2 + 15120n8K
1 - 15120n8K
2 + 66640n9 + 2352n10 + 781760n8) | |
|
| c[6] | = -2520(2n + 11)(2n + 9)(2n + 5)(2n + 3)(n + 5)(n + 4)(2n + 7)2(K
2 + K1)(-14n2K
1 - 98nK1 - 90K1 + 45K1K2 - 4n4 - 56n3 - 240n2 - 308n - 135 + 14n2K
2 + 98nK2 + 90K2)(n + 1) | |
|
| c[7] | = -(2n + 11)(2n + 9)(2n + 7)(2n + 5)(2n + 3)(2n + 1)(n + 5)(n + 4)(893025 + 4190760n + 1190700K1 - 1190700K2 + 21952n7 + 8617168n3 + 4775416n4 + 8439072n2 + 249088n6 - 1389150K
1K2 + 396900K22 + 396900K
1K22 + 99225K
12K
22 + 396900K
12 + 1466080n5 - 396900K
12K
2 - 396900nK12K
2 + 5241060n2K
1 + 4088700nK1 + 855540nK22 + 855540nK
12 + 554400n2K
12 - 4088700nK
2 - 3059280n3K
2 + 8820n4K
12 + 56700n2K
1K22 + 396900nK
1K22 - 56700n2K
12K
2 + 554400n2K
22 - 5241060n2K
2 + 123480n3K
12 + 3059280n3K
1 + 123480n3K
22 + 105840n5K
1 + 835920n4K
1 + 8820n4K
22 - 835920n4K
2 - 105840n5K
2 - 5040n6K
2 + 5040n6K
1 - 2948400nK1K2 - 2008800n2K
1K2 - 453600n3K
1K2 - 32400n4K
1K2 + 784n8) | | |
Expressions for all quantities involved are provided below.
Psi_1:=-320*K_1+320*K_2-240*x^4+160*x*K_2+160*x*K_1+480*K_1*x^2+80*K_1*K_2-160*K_2*x^3-160*K_1*x^3-160*K_1*x^4+160*K_2*x^4-480*K_2*x^2+80*K_1*K_2*x^4-160*K_1*K_2*x^2-1200+1440*x^2;
Psi_2:=26800*K_1*K_2^2*x^3+14800*x*K_1^2*K_2-943320*x-27680*K_1-27680*K_2-4400*K_1^2*K_2*x^2-249600*K_1*K_2*x^3+153200*x*K_1*K_2-14800*x*K_1*K_2^2-1400*x*K_1^2*K_2^2+1347600*x^3-12000*K_1*K_2^2*x^5-26800*K_1^2*K_2*x^3+2800*K_1^2*K_2^2*x^3+388400*x*K_2-388400*x*K_1+87120*K_1*x^2-1400*K_1^2*K_2^2*x^5+96400*K_1*K_2*x^5+12000*K_1^2*K_2*x^5+4960*K_2^2+800*K_1*K_2^2+3600*K_1^2*K_2*x^4+3600*K_1*K_2^2*x^4-593360*K_2*x^3+593360*K_1*x^3-59440*K_1*x^4-59440*K_2*x^4+87120*K_2*x^2-4400*K_1*K_2^2*x^2-4960*K_1^2-404280*x^5-38560*x*K_1^2-21120*K_2^2*x^2+21120*K_1^2*x^2-38560*x*K_2^2+65920*K_2^2*x^3+65920*K_1^2*x^3+16160*K_2^2*x^4-16160*K_1^2*x^4-204960*K_1*x^5+204960*K_2*x^5-27360*K_2^2*x^5-27360*K_1^2*x^5+800*K_1^2*K_2;
c[1]:=64*(n+8)*(n+3)*(61425+45720*n+18900*K_1-18900*K_2+15680*n^7-81040*n^3+467896*n^4-123456*n^2+117376*n^6-28350*K_1*K_2-18900*K_2^2+56700*K_1*K_2^2+99225*K_1^2*K_2^2-18900*K_1^2+388640*n^5-56700*K_1^2*K_2-283500*n*K_1^2*K_2+95940*n^2*K_1-60300*n*K_1+81900*n*K_2^2+81900*n*K_1^2+236880*n^2*K_1^2+60300*n*K_2-673200*n^3*K_2+8820*n^4*K_1^2+56700*n^2*K_1*K_2^2+283500*n*K_1*K_2^2-56700*n^2*K_1^2*K_2+236880*n^2*K_2^2-95940*n^2*K_2+88200*n^3*K_1^2+673200*n^3*K_1+88200*n^3*K_2^2+75600*n^5*K_1+382320*n^4*K_1+8820*n^4*K_2^2-382320*n^4*K_2-75600*n^5*K_2-5040*n^6*K_2+5040*n^6*K_1-162000*n*K_1*K_2-842400*n^2*K_1*K_2-324000*n^3*K_1*K_2-32400*n^4*K_1*K_2+784*n^8)*(n+7)*(n+2)^2*n*(n+1)^2;
c[2]:=-40320*(n+7)*(n+2)^2*n*(n+1)^2*(2*n+11)*(2*n+5)*(n+5)*(K_2+K_1)*(-14*n^2*K_1-70*n*K_1+45*K_1*K_2-6*K_1-4*n^4-40*n^3-96*n^2+20*n-15+14*n^2*K_2+70*n*K_2+6*K_2);
c[3]:=-16*(n+1)^2*n*(n+4)*(2*n+11)*(2*n+9)*(-1256850+1955835*n+4498200*K_1-4498200*K_2+7225120*n^7+88252280*n^3+115141760*n^4+31313067*n^2+30973256*n^6-22623300*K_1*K_2+3439800*K_2^2+13494600*K_1*K_2^2+26460*n^6*K_2^2+7739550*K_1^2*K_2^2+26460*n^6*K_1^2+3439800*K_1^2+78963160*n^5-13494600*K_1^2*K_2-27726300*n*K_1^2*K_2+91714680*n^2*K_1+33484500*n*K_1+19246500*n*K_2^2+19246500*n*K_1^2+28035000*n^2*K_1^2-33484500*n*K_2-115006320*n^3*K_2+4238640*n^4*K_1^2+2494800*n^3*K_1*K_2^2+13267800*n^2*K_1*K_2^2+27726300*n*K_1*K_2^2-13267800*n^2*K_1^2*K_2+28035000*n^2*K_2^2-91714680*n^2*K_2+538020*n^5*K_1^2+15917580*n^3*K_1^2+115006320*n^3*K_1+15917580*n^3*K_2^2-2494800*n^3*K_1^2*K_2+23124960*n^5*K_1+70508700*n^4*K_1+4238640*n^4*K_2^2-70508700*n^4*K_2+538020*n^5*K_2^2-23124960*n^5*K_2-4176000*n^6*K_2+4176000*n^6*K_1+393120*n^7*K_1-393120*n^7*K_2+2679075*n*K_1^2*K_2^2-80825850*n*K_1*K_2+297675*n^2*K_1^2*K_2^2-111022650*n^2*K_1*K_2-60620400*n^3*K_1*K_2-170100*n^4*K_1^2*K_2+170100*n^4*K_1*K_2^2-15746400*n^4*K_1*K_2-1976400*n^5*K_1*K_2-97200*n^6*K_1*K_2+15120*n^8*K_1-15120*n^8*K_2+74480*n^9+2352*n^10+993440*n^8);
c[4]:=20160*(n+5)*(2*n+11)*(2*n+9)*(2*n+7)*(K_2+K_1)*(-28*n^4*K_1-336*n^3*K_1-1132*n^2*K_1+90*n^2*K_1*K_2-744*n*K_1+540*n*K_1*K_2+315*K_1*K_2+350*K_1-8*n^6-144*n^5-900*n^4-2160*n^3-1122*n^2+1044*n+455+28*n^4*K_2+336*n^3*K_2+1132*n^2*K_2+744*n*K_2-350*K_2)*(n+1)*n*(n+3);
c[5]:=4*(n+2)*(2*n+11)*(2*n+9)*(2*n+7)*(2*n+5)*(n+5)*(2381400+9770985*n+6350400*K_1-6350400*K_2+4897760*n^7+35114440*n^3+45389840*n^4+21852987*n^2+17660936*n^6-14288400*K_1*K_2+3175200*K_2^2+6350400*K_1*K_2^2+26460*n^6*K_2^2+2381400*K_1^2*K_2^2+26460*n^6*K_1^2+3175200*K_1^2+37113800*n^5-6350400*K_1^2*K_2-9015300*n*K_1^2*K_2+40367160*n^2*K_1+22852620*n*K_1+8407980*n*K_2^2+8407980*n*K_1^2+9324000*n^2*K_1^2-22852620*n*K_2-44708400*n^3*K_2+2386440*n^4*K_1^2+1587600*n^3*K_1*K_2^2+5103000*n^2*K_1*K_2^2+9015300*n*K_1*K_2^2-5103000*n^2*K_1^2*K_2+9324000*n^2*K_2^2-40367160*n^2*K_2+414540*n^5*K_1^2+6429780*n^3*K_1^2+44708400*n^3*K_1+6429780*n^3*K_2^2-1587600*n^3*K_1^2*K_2+12903840*n^5*K_1+31499100*n^4*K_1+2386440*n^4*K_2^2-31499100*n^4*K_2+414540*n^5*K_2^2-12903840*n^5*K_2-2905920*n^6*K_2+2905920*n^6*K_1+332640*n^7*K_1-332640*n^7*K_2+893025*n*K_1^2*K_2^2-37223550*n*K_1*K_2+297675*n^2*K_1^2*K_2^2-41621850*n^2*K_1*K_2-25693200*n^3*K_1*K_2-170100*n^4*K_1^2*K_2+170100*n^4*K_1*K_2^2-8942400*n^4*K_1*K_2-1522800*n^5*K_1*K_2-97200*n^6*K_1*K_2+15120*n^8*K_1-15120*n^8*K_2+66640*n^9+2352*n^10+781760*n^8);
c[6]:=-2520*(2*n+11)*(2*n+9)*(2*n+5)*(2*n+3)*(n+5)*(n+4)*(2*n+7)^2*(K_2+K_1)*(-14*n^2*K_1-98*n*K_1-90*K_1+45*K_1*K_2-4*n^4-56*n^3-240*n^2-308*n-135+14*n^2*K_2+98*n*K_2+90*K_2)*(n+1);
c[7]:=-(2*n+11)*(2*n+9)*(2*n+7)*(2*n+5)*(2*n+3)*(2*n+1)*(n+5)*(n+4)*(893025+4190760*n+1190700*K_1-1190700*K_2+21952*n^7+8617168*n^3+4775416*n^4+8439072*n^2+249088*n^6-1389150*K_1*K_2+396900*K_2^2+396900*K_1*K_2^2+99225*K_1^2*K_2^2+396900*K_1^2+1466080*n^5-396900*K_1^2*K_2-396900*n*K_1^2*K_2+5241060*n^2*K_1+4088700*n*K_1+855540*n*K_2^2+855540*n*K_1^2+554400*n^2*K_1^2-4088700*n*K_2-3059280*n^3*K_2+8820*n^4*K_1^2+56700*n^2*K_1*K_2^2+396900*n*K_1*K_2^2-56700*n^2*K_1^2*K_2+554400*n^2*K_2^2-5241060*n^2*K_2+123480*n^3*K_1^2+3059280*n^3*K_1+123480*n^3*K_2^2+105840*n^5*K_1+835920*n^4*K_1+8820*n^4*K_2^2-835920*n^4*K_2-105840*n^5*K_2-5040*n^6*K_2+5040*n^6*K_1-2948400*n*K_1*K_2-2008800*n^2*K_1*K_2-453600*n^3*K_1*K_2-32400*n^4*K_1*K_2+784*n^8);
Case(ii) α = β = 1∕2
The ‘starting’ functions are given by
| Ψ1 | = -600 - 160K1 + 160K2 + 40K1K2 + 720x2 - 120x4 - 80K
1K2x2 + 80xK
2 + 80xK1 + 240K1x2 - 240K
2x2 - 80K
2x3 - 80K
1x3 - 80K
1x4 + 40K
1K2x4 + 80K
2x4 | |
|
| Ψ2 | = -799260x - 17840K1 - 17840K2 + 3280K22 + 560K
1K22 - 342540x5 - 3280K
12 + 134680xK
1K2 - 13160xK1K22 - 33520xK
22 - 33520xK
12 - 16640K
22x2 - 1260xK
12K
22 + 13160xK
12K
2 - 3640K1K22x2 - 3640K
12K
2x2 + 16640K
12x2 + 56960K
22x3 + 2520K
12K
22x3 + 23800K
1K22x3 - 23800K
12K
2x3 - 219520K
1K2x3 + 3080K
1K22x4 + 3080K
12K
2x4 + 56960K
12x3 + 13360K
22x4 - 13360K
12x4 - 23440K
22x5 - 23440K
12x5 - 175920K
1x5 + 175920K
2x5 - 10640K
1K22x5 + 10640K
12K
2x5 - 1260K
12K
22x5 + 84840K
1K2x5 + 560K
12K
2 + 1141800x3 + 334360xK
2 - 334360xK1 + 67080K1x2 + 67080K
2x2 - 510280K
2x3 + 510280K
1x3 - 49240K
1x4 - 49240K
2x4 | | |
| c[1] | = 64(n + 10)(286209 + 83272n + 19404K1 - 19404K2 + 36288n7 - 232624n3 + 3130360n4 - 1148032n2 + 381312n6 + 106722K
1K2 - 97020K22 + 213444K
1K22 + 480249K
12K
22 - 97020K
12 + 1784160n5 - 213444K
12K
2 - 1494108nK12K
2 + 513436n2K
1 - 631708nK1 + 368676nK22 + 368676nK
12 + 1275120n2K
12 + 631708nK
2 - 3975664n3K
2 + 24948n4K
12 + 213444n2K
1K22 + 1494108nK
1K22 - 213444n2K
12K
2 + 1275120n2K
22 - 513436n2K
2 + 349272n3K
12 + 3975664n3K
1 + 349272n3K
22 + 232848n5K
1 + 1642256n4K
1 + 24948n4K
22 - 1642256n4K
2 - 232848n5K
2 - 11088n6K
2 + 11088n6K
1 - 664048nK1K2 - 4743200n2K
1K2 - 1328096n3K
1K2 - 94864n4K
1K2 + 1296n8)(n + 9)(n + 3)2(n + 2)2(n + 1)n | |
|
| c[2] | = -88704(n + 9)(n + 2)2(n + 1)n(n + 3)(2n + 7)(n + 6)(2n + 13)(-4n4 - 56n3 - 18n2K
1 + 18n2K
2 - 192n2 - 126nK
1 + 126nK2 + 28n + 77K1K2 - 10K1 + 10K2 - 7)(K2 + K1) | |
|
| c[3] | = -48(n + 5)(2n + 13)(2n + 11)(-12137202 - 24726303n + 349272K1 - 349272K2 + 9602976n7 + 276941400n3 + 339784096n4 + 67227913n2 + 55242328n6 - 48024900K
1K2 + 5937624K22 + 34577928K
1K22 + 24948n6K
22 + 22091454K
12K
22 + 24948n6K
12 + 5937624K
12 + 186052968n5 - 34577928K
12K
2 - 80468388nK12K
2 + 264780824n2K
1 + 72290988nK1 + 54051228nK22 + 54051228nK
12 + 80927616n2K
12 - 72290988nK
2 - 329703528n3K
2 + 7096320n4K
12 + 4126584n3K
1K22 + 29170680n2K
1K22 + 80468388nK
1K22 - 29170680n2K
12K
2 + 80927616n2K
22 - 264780824n2K
2 + 673596n5K
12 + 35704284n3K
12 + 329703528n3K
1 + 35704284n3K
22 - 4126584n3K
12K
2 + 40426848n5K
1 + 162567020n4K
1 + 7096320n4K
22 - 162567020n4K
2 + 673596n5K
22 - 40426848n5K
2 - 5460224n6K
2 + 5460224n6K
1 + 384384n7K
1 - 384384n7K
2 + 5602905nK12K
22 - 219313710nK
1K2 + 480249n2K
12K
22 - 317877406n2K
1K2 - 138027120n3K
1K2 - 213444n4K
12K
2 + 213444n4K
1K22 - 27131104n4K
1K2 - 2561328n5K
1K2 - 94864n6K
1K2 + 11088n8K
1 - 11088n8K
2 + 54864n9 + 1296n10 + 981792n8)(n + 2)n(n + 1) | |
|
| c[4] | = 88704(n + 2)n(2n + 11)(2n + 9)(n + 6)(n + 4)(2n + 13)(K2 + K1)(-18n4K
1 - 288n3K
1 - 1333n2K
1 + 77n2K
1K2 - 1448nK1 + 616nK1K2 + 315K1 + 693K1K2 - 4n6 - 96n5 - 808n4 - 2688n3 - 2401n2 + 1272n + 567 + 18n4K
2 + 288n3K
2 + 1333n2K
2 + 1448nK2 - 315K2) | |
|
| c[5] | = 12(n + 3)(2n + 11)(2n + 9)(2n + 7)(n + 6)(2n + 13)(-4802490 - 1893969n + 6403320K1 - 6403320K2 + 6451296n7 + 155755944n3 + 168756064n4 + 57125065n2 + 32023384n6 - 35218260K
1K2 + 6403320K22 + 19209960K
1K22 + 24948n6K
22 + 8004150K
12K
22 + 24948n6K
12 + 6403320K
12 + 95794968n5 - 19209960K
12K
2 - 31091676nK12K
2 + 149214296n2K
1 + 58310868nK1 + 28561764nK22 + 28561764nK
12 + 33005280n2K
12 - 58310868nK
2 - 153230616n3K
2 + 4102560n4K
12 + 2703624n3K
1K22 + 12095160n2K
1K22 + 31091676nK
1K22 - 12095160n2K
12K
2 + 33005280n2K
22 - 149214296n2K
2 + 523908n5K
12 + 15744036n3K
12 + 153230616n3K
1 + 15744036n3K
22 - 2703624n3K
12K
2 + 22966944n5K
1 + 78298220n4K
1 + 4102560n4K
22 - 78298220n4K
2 + 523908n5K
22 - 22966944n5K
2 - 3804416n6K
2 + 3804416n6K
1 + 325248n7K
1 - 325248n7K
2 + 2081079nK12K
22 - 125042610nK
1K2 + 480249n2K
12K
22 - 138015262n2K
1K2 - 62325648n3K
1K2 - 213444n4K
12K
2 + 213444n4K
1K22 - 15747424n4K
1K2 - 1992144n5K
1K2 - 94864n6K
1K2 + 11088n8K
1 - 11088n8K
2 + 48816n9 + 1296n10 + 764064n8) | |
|
| c[6] | = -5544(n + 2)(2n + 11)(2n + 7)(2n + 5)(n + 6)(n + 5)(2n + 13)(2n + 9)2(K
2 + K1)(-18n2K
1 - 162nK1 - 154K1 + 77K1K2 - 4n4 - 72n3 - 384n2 - 540n - 231 + 18n2K
2 + 162nK2 + 154K2) | |
|
| c[7] | = -(2n + 11)(2n + 9)(2n + 7)(2n + 5)(2n + 3)(n + 6)(n + 5)(2n + 13)(4322241 + 21083832n + 5762988K1 - 5762988K2 + 46656n7 + 39099312n3 + 19131640n4 + 41295872n2 + 671616n6 - 6723486K
1K2 + 1920996K22 + 1920996K
1K22 + 480249K
12K
22 + 1920996K
12 + 4906656n5 - 1920996K
12K
2 - 1920996nK12K
2 + 24788764n2K
1 + 20121948nK1 + 4066524nK22 + 4066524nK
12 + 2472624n2K
12 - 20121948nK
2 - 13094928n3K
2 + 24948n4K
12 + 213444n2K
1K22 + 1920996nK
1K22 - 213444n2K
12K
2 + 2472624n2K
22 - 24788764n2K
2 + 449064n3K
12 + 13094928n3K
1 + 449064n3K
22 + 299376n5K
1 + 2972816n4K
1 + 24948n4K
22 - 2972816n4K
2 - 299376n5K
2 - 11088n6K
2 + 11088n6K
1 - 14514192nK1K2 - 9296672n2K
1K2 - 1707552n3K
1K2 - 94864n4K
1K2 + 1296n8) | | |
Expressions for all quantities involved are provided below.
Psi_1:=-600-160*K_1+160*K_2+40*K_1*K_2-80*K_1*K_2*x^2+40*K_1*K_2*x^4+720*x^2-120*x^4+80*x*K_2+80*x*K_1+240*K_1*x^2-240*K_2*x^2-80*K_2*x^3-80*K_1*x^3-80*K_1*x^4+80*K_2*x^4;
Psi_2:=-799260*x-17840*K_1-17840*K_2-13160*x*K_1*K_2^2-1260*x*K_1^2*K_2^2-3640*K_1*K_2^2*x^2+13160*x*K_1^2*K_2+134680*x*K_1*K_2+3280*K_2^2+560*K_1*K_2^2-3640*K_1^2*K_2*x^2-219520*K_1*K_2*x^3-23800*K_1^2*K_2*x^3+23800*K_1*K_2^2*x^3+2520*K_1^2*K_2^2*x^3+3080*K_1^2*K_2*x^4+3080*K_1*K_2^2*x^4-1260*K_1^2*K_2^2*x^5-10640*K_1*K_2^2*x^5+10640*K_1^2*K_2*x^5+84840*K_1*K_2*x^5-3280*K_1^2-342540*x^5-33520*x*K_2^2-33520*x*K_1^2-16640*K_2^2*x^2+16640*K_1^2*x^2+56960*K_2^2*x^3+560*K_1^2*K_2+56960*K_1^2*x^3-13360*K_1^2*x^4+13360*K_2^2*x^4-23440*K_1^2*x^5-23440*K_2^2*x^5-175920*K_1*x^5+175920*K_2*x^5+1141800*x^3+334360*x*K_2-334360*x*K_1+67080*K_1*x^2+67080*K_2*x^2-510280*K_2*x^3+510280*K_1*x^3-49240*K_1*x^4-49240*K_2*x^4;
c[1]:=64*(n+10)*(286209+83272*n+19404*K_1-19404*K_2+36288*n^7-232624*n^3+3130360*n^4-1148032*n^2+381312*n^6+106722*K_1*K_2-97020*K_2^2+213444*K_1*K_2^2+480249*K_1^2*K_2^2-97020*K_1^2+1784160*n^5-213444*K_1^2*K_2-1494108*n*K_1^2*K_2+513436*n^2*K_1-631708*n*K_1+368676*n*K_2^2+368676*n*K_1^2+1275120*n^2*K_1^2+631708*n*K_2-3975664*n^3*K_2+24948*n^4*K_1^2+213444*n^2*K_1*K_2^2+1494108*n*K_1*K_2^2-213444*n^2*K_1^2*K_2+1275120*n^2*K_2^2-513436*n^2*K_2+349272*n^3*K_1^2+3975664*n^3*K_1+349272*n^3*K_2^2+232848*n^5*K_1+1642256*n^4*K_1+24948*n^4*K_2^2-1642256*n^4*K_2-232848*n^5*K_2-11088*n^6*K_2+11088*n^6*K_1-664048*n*K_1*K_2-4743200*n^2*K_1*K_2-1328096*n^3*K_1*K_2-94864*n^4*K_1*K_2+1296*n^8)*(n+9)*(n+3)^2*(n+2)^2*(n+1)*n;
c[2]:=-88704*(n+9)*(n+2)^2*(n+1)*n*(n+3)*(2*n+7)*(n+6)*(2*n+13)*(-4*n^4-56*n^3-18*n^2*K_1+18*n^2*K_2-192*n^2-126*n*K_1+126*n*K_2+28*n+77*K_1*K_2-10*K_1+10*K_2-7)*(K_2+K_1);
c[3]:=-48*(n+5)*(2*n+13)*(2*n+11)*(-12137202-24726303*n+349272*K_1-349272*K_2+9602976*n^7+276941400*n^3+339784096*n^4+67227913*n^2+55242328*n^6-48024900*K_1*K_2+5937624*K_2^2+34577928*K_1*K_2^2+24948*n^6*K_2^2+22091454*K_1^2*K_2^2+24948*n^6*K_1^2+5937624*K_1^2+186052968*n^5-34577928*K_1^2*K_2-80468388*n*K_1^2*K_2+264780824*n^2*K_1+72290988*n*K_1+54051228*n*K_2^2+54051228*n*K_1^2+80927616*n^2*K_1^2-72290988*n*K_2-329703528*n^3*K_2+7096320*n^4*K_1^2+4126584*n^3*K_1*K_2^2+29170680*n^2*K_1*K_2^2+80468388*n*K_1*K_2^2-29170680*n^2*K_1^2*K_2+80927616*n^2*K_2^2-264780824*n^2*K_2+673596*n^5*K_1^2+35704284*n^3*K_1^2+329703528*n^3*K_1+35704284*n^3*K_2^2-4126584*n^3*K_1^2*K_2+40426848*n^5*K_1+162567020*n^4*K_1+7096320*n^4*K_2^2-162567020*n^4*K_2+673596*n^5*K_2^2-40426848*n^5*K_2-5460224*n^6*K_2+5460224*n^6*K_1+384384*n^7*K_1-384384*n^7*K_2+5602905*n*K_1^2*K_2^2-219313710*n*K_1*K_2+480249*n^2*K_1^2*K_2^2-317877406*n^2*K_1*K_2-138027120*n^3*K_1*K_2-213444*n^4*K_1^2*K_2+213444*n^4*K_1*K_2^2-27131104*n^4*K_1*K_2-2561328*n^5*K_1*K_2-94864*n^6*K_1*K_2+11088*n^8*K_1-11088*n^8*K_2+54864*n^9+1296*n^10+981792*n^8)*(n+2)*n*(n+1);
c[4]:=88704*(n+2)*n*(2*n+11)*(2*n+9)*(n+6)*(n+4)*(2*n+13)*(K_2+K_1)*(-18*n^4*K_1-288*n^3*K_1-1333*n^2*K_1+77*n^2*K_1*K_2-1448*n*K_1+616*n*K_1*K_2+315*K_1+693*K_1*K_2-4*n^6-96*n^5-808*n^4-2688*n^3-2401*n^2+1272*n+567+18*n^4*K_2+288*n^3*K_2+1333*n^2*K_2+1448*n*K_2-315*K_2);
c[5]:=12*(n+3)*(2*n+11)*(2*n+9)*(2*n+7)*(n+6)*(2*n+13)*(-4802490-1893969*n+6403320*K_1-6403320*K_2+6451296*n^7+155755944*n^3+168756064*n^4+57125065*n^2+32023384*n^6-35218260*K_1*K_2+6403320*K_2^2+19209960*K_1*K_2^2+24948*n^6*K_2^2+8004150*K_1^2*K_2^2+24948*n^6*K_1^2+6403320*K_1^2+95794968*n^5-19209960*K_1^2*K_2-31091676*n*K_1^2*K_2+149214296*n^2*K_1+58310868*n*K_1+28561764*n*K_2^2+28561764*n*K_1^2+33005280*n^2*K_1^2-58310868*n*K_2-153230616*n^3*K_2+4102560*n^4*K_1^2+2703624*n^3*K_1*K_2^2+12095160*n^2*K_1*K_2^2+31091676*n*K_1*K_2^2-12095160*n^2*K_1^2*K_2+33005280*n^2*K_2^2-149214296*n^2*K_2+523908*n^5*K_1^2+15744036*n^3*K_1^2+153230616*n^3*K_1+15744036*n^3*K_2^2-2703624*n^3*K_1^2*K_2+22966944*n^5*K_1+78298220*n^4*K_1+4102560*n^4*K_2^2-78298220*n^4*K_2+523908*n^5*K_2^2-22966944*n^5*K_2-3804416*n^6*K_2+3804416*n^6*K_1+325248*n^7*K_1-325248*n^7*K_2+2081079*n*K_1^2*K_2^2-125042610*n*K_1*K_2+480249*n^2*K_1^2*K_2^2-138015262*n^2*K_1*K_2-62325648*n^3*K_1*K_2-213444*n^4*K_1^2*K_2+213444*n^4*K_1*K_2^2-15747424*n^4*K_1*K_2-1992144*n^5*K_1*K_2-94864*n^6*K_1*K_2+11088*n^8*K_1-11088*n^8*K_2+48816*n^9+1296*n^10+764064*n^8);
c[6]:=-5544*(n+2)*(2*n+11)*(2*n+7)*(2*n+5)*(n+6)*(n+5)*(2*n+13)*(2*n+9)^2*(K_2+K_1)*(-18*n^2*K_1-162*n*K_1-154*K_1+77*K_1*K_2-4*n^4-72*n^3-384*n^2-540*n-231+18*n^2*K_2+162*n*K_2+154*K_2);
c[7]:=-(2*n+11)*(2*n+9)*(2*n+7)*(2*n+5)*(2*n+3)*(n+6)*(n+5)*(2*n+13)*(4322241+21083832*n+5762988*K_1-5762988*K_2+46656*n^7+39099312*n^3+19131640*n^4+41295872*n^2+671616*n^6-6723486*K_1*K_2+1920996*K_2^2+1920996*K_1*K_2^2+480249*K_1^2*K_2^2+1920996*K_1^2+4906656*n^5-1920996*K_1^2*K_2-1920996*n*K_1^2*K_2+24788764*n^2*K_1+20121948*n*K_1+4066524*n*K_2^2+4066524*n*K_1^2+2472624*n^2*K_1^2-20121948*n*K_2-13094928*n^3*K_2+24948*n^4*K_1^2+213444*n^2*K_1*K_2^2+1920996*n*K_1*K_2^2-213444*n^2*K_1^2*K_2+2472624*n^2*K_2^2-24788764*n^2*K_2+449064*n^3*K_1^2+13094928*n^3*K_1+449064*n^3*K_2^2+299376*n^5*K_1+2972816*n^4*K_1+24948*n^4*K_2^2-2972816*n^4*K_2-299376*n^5*K_2-11088*n^6*K_2+11088*n^6*K_1-14514192*n*K_1*K_2-9296672*n^2*K_1*K_2-1707552*n^3*K_1*K_2-94864*n^4*K_1*K_2+1296*n^8);
Case(iii) α = β = 0
The ‘starting’ functions are given by
| Ψ1 | = -396K1 + 396K2 + 99K1K2 + 1782x2 - 297x4 - 594K
2x2 + 198xK
2 + 198xK1 + 594K1x2 + 198K
2x4 - 198K
1x3 - 198K
1x4 - 198K
2x3 - 1485 + 99K
1K2x4 - 198K
1K2x2 | |
|
| Ψ2 | = -128898x - 3267K1 - 3267K2 - 2178K12x4 + 2178K
22x4 - 3762K
12x5 - 3762K
22x5 + 28215K
2x5 - 28215K
1x5 + 594K
22 + 99K
1K22 - 594K
12 + 184140x3 + 11286K
2x2 + 53559xK
2 - 53559xK1 + 11286K1x2 - 8019K
2x4 + 81774K
1x3 - 8019K
1x4 - 81774K
2x3 + 99K
12K
2 + 21384xK1K2 - 2079xK1K22 + 2079xK
12K
2 - 198xK12K
22 - 594K
1K22x2 - 594K
12K
2x2 + 3762K
1K22x3 + 396K
12K
22x3 - 34848K
1K2x3 - 3762K
12K
2x3 + 495K
12K
2x4 + 495K
1K22x4 + 13464K
1K2x5 - 1683K
1K22x5 + 1683K
12K
2x5 - 198K
12K
22x5 - 55242x5 - 5346xK
22 - 5346xK
12 - 2772K
22x2 + 2772K
12x2 + 9108K
22x3 + 9108K
12x3 | | |
| c[1] | = (2n + 5)(n + 8)(n + 1)n(2n + 3)(n + 3)(n + 2)(n + 9)(540 + 264n + 90K1 - 90K2 + 96n7 - 576n3 + 5136n4 - 1684n2 + 864n6 - 180K
22 + 450K
1K22 + 900K
12K
22 - 180K
12 + 3456n5 - 450K
12K
2 - 2700nK12K
2 + 930n2K
1 - 900nK1 + 720nK22 + 720nK
12 + 2280n2K
12 + 900nK
2 - 6840n3K
2 + 60n4K
12 + 450n2K
1K22 + 2700nK
1K22 - 450n2K
12K
2 + 2280n2K
22 - 930n2K
2 + 720n3K
12 + 6840n3K
1 + 720n3K
22 + 540n5K
1 + 3270n4K
1 + 60n4K
22 - 3270n4K
2 - 540n5K
2 - 30n6K
2 + 30n6K
1 - 1350nK1K2 - 8325n2K
1K2 - 2700n3K
1K2 - 225n4K
1K2 + 4n8) | |
|
| c[2] | = -30(n + 6)(2n + 11)(K2 + K1)(-4n2K
1 - 24nK1 - 2K1 + 15K1K2 - n4 - 12n3 - 35n2 + 6n - 3 + 4n2K
2 + 24nK2 + 2K2)(2n + 5)(n + 8)(n + 1)n(2n + 3)(n + 3)(n + 2) | |
|
| c[3] | = -3(n + 1)n(2n + 3)(n + 5)(2n + 9)(n + 6)(-12600 - 17340n + 7800K1 - 7800K2 + 19728n7 + 382412n3 + 483548n4 + 109612n2 + 99144n6 - 79200K
1K2 + 10800K22 + 52200K
1K22 + 60n6K
22 + 31800K
12K
22 + 60n6K
12 + 10800K
12 + 293832n5 - 52200K
12K
2 - 114900nK12K
2 + 378980n2K
1 + 118360nK1 + 78400nK22 + 78400nK
12 + 115920n2K
12 - 118360nK
2 - 473660n3K
2 + 13080n4K
12 + 7650n3K
1K22 + 47400n2K
1K22 + 114900nK
1K22 - 47400n2K
12K
2 + 115920n2K
22 - 378980n2K
2 + 1420n5K
12 + 57520n3K
12 + 473660n3K
1 + 57520n3K
22 - 7650n3K
12K
2 + 73160n5K
1 + 258800n4K
1 + 13080n4K
22 - 258800n4K
2 + 1420n5K
22 - 73160n5K
2 - 11300n6K
2 + 11300n6K
1 + 910n7K
1 - 910n7K
2 + 9300nK12K
22 - 322800nK
1K2 + 900n2K
12K
22 - 456150n2K
1K2 - 220875n3K
1K2 - 450n4K
12K
2 + 450n4K
1K22 - 49425n4K
1K2 - 5325n5K
1K2 - 225n6K
1K2 + 30n8K
1 - 30n8K
2 + 148n9 + 4n10 + 2312n8) | |
|
| c[4] | = 60(2n + 11)(2n + 7)(n + 6)(n + 5)(n + 4)(K2 + K1)(-4n4K
1 - 56n3K
1 - 224n2K
1 + 15n2K
1K2 - 196nK1 + 105nK1K2 + 60K1 + 90K1K2 - n6 - 21n5 - 154n4 - 441n3 - 313n2 + 210n + 90 + 4n4K
2 + 56n3K
2 + 224n2K
2 + 196nK2 - 60K2)n(2n + 3) | |
|
| c[5] | = 3(n + 5)(n + 4)(2n + 11)(n + 6)(15660n + 16200K1 - 16200K2 + 13312n7 + 188788n3 + 221692n4 + 83796n2 + 57200n6 - 54000K
1K2 + 10800K22 + 27000K
1K22 + 60n6K
22 + 10800K
12K
22 + 60n6K
12 + 10800K
12 + 146608n5 - 27000K
12K
2 - 41550nK12K
2 + 193410n2K
1 + 87930nK1 + 38220nK22 + 38220nK
12 + 43820n2K
12 - 87930nK
2 - 206250n3K
2 + 7480n4K
12 + 4950n3K
1K22 + 19050n2K
1K22 + 41550nK
1K22 - 19050n2K
12K
2 + 43820n2K
22 - 193410n2K
2 + 1100n5K
12 + 24520n3K
12 + 206250n3K
1 + 24520n3K
22 - 4950n3K
12K
2 + 41290n5K
1 + 121250n4K
1 + 7480n4K
22 - 121250n4K
2 + 1100n5K
22 - 41290n5K
2 - 7870n6K
2 + 7870n6K
1 + 770n7K
1 - 770n7K
2 + 3300nK12K
22 - 168600nK
1K2 + 900n2K
12K
22 - 187350n2K
1K2 - 97275n3K
1K2 - 450n4K
12K
2 + 450n4K
1K22 - 28425n4K
1K2 - 4125n5K
1K2 - 225n6K
1K2 + 30n8K
1 - 30n8K
2 + 132n9 + 4n10 + 1808n8)(2n + 5)(n + 3) | |
|
| c[6] | = -30(n + 5)(2n + 11)(2n + 9)(n + 6)(n + 4)2(K
2 + K1)(-4n2K
1 - 32nK1 - 30K1 + 15K1K2 - n4 - 16n3 - 77n2 - 104n - 45 + 4n2K
2 + 32nK2 + 30K2)(2n + 3)(n + 3)(n + 2) | |
|
| c[7] | = -(n + 5)(n + 4)(2n + 11)(2n + 9)(n + 6)(8100 + 38880n + 10800K1 - 10800K2 + 128n7 + 75392n3 + 39016n4 + 77052n2 + 1648n6 - 12600K
1K2 + 3600K22 + 3600K
1K22 + 900K
12K
22 + 3600K
12 + 10880n5 - 3600K
12K
2 - 3600nK12K
2 + 46920n2K
1 + 37440nK1 + 7680nK22 + 7680nK
12 + 4800n2K
12 - 37440nK
2 - 25920n3K
2 + 60n4K
12 + 450n2K
1K22 + 3600nK
1K22 - 450n2K
12K
2 + 4800n2K
22 - 46920n2K
2 + 960n3K
12 + 25920n3K
1 + 960n3K
22 + 720n5K
1 + 6420n4K
1 + 60n4K
22 - 6420n4K
2 - 720n5K
2 - 30n6K
2 + 30n6K
1 - 27000nK1K2 - 17775n2K
1K2 - 3600n3K
1K2 - 225n4K
1K2 + 4n8)(n + 1)(n + 3)(n + 2) | | |
Expressions for all quantities involved are provided below.
Psi_1:=-396*K_1+396*K_2+99*K_1*K_2+99*K_1*K_2*x^4-198*K_1*K_2*x^2+1782*x^2-297*x^4+198*x*K_2+198*x*K_1+594*K_1*x^2+198*K_2*x^4-198*K_1*x^4-198*K_2*x^3-198*K_1*x^3-594*K_2*x^2-1485;
Psi_2:=-128898*x-3267*K_1-3267*K_2+495*K_1*K_2^2*x^4+495*K_1^2*K_2*x^4-3762*K_1^2*K_2*x^3+396*K_1^2*K_2^2*x^3-34848*K_1*K_2*x^3+3762*K_1*K_2^2*x^3-594*K_1^2*K_2*x^2-594*K_1*K_2^2*x^2+2079*x*K_1^2*K_2-198*x*K_1^2*K_2^2-2079*x*K_1*K_2^2+21384*x*K_1*K_2+594*K_2^2+99*K_1*K_2^2+1683*K_1^2*K_2*x^5-1683*K_1*K_2^2*x^5+13464*K_1*K_2*x^5-198*K_1^2*K_2^2*x^5+184140*x^3+53559*x*K_2-53559*x*K_1+11286*K_1*x^2-8019*K_2*x^4-8019*K_1*x^4-81774*K_2*x^3+81774*K_1*x^3+11286*K_2*x^2-594*K_1^2-55242*x^5+99*K_1^2*K_2-5346*x*K_2^2-5346*x*K_1^2-2772*K_2^2*x^2+2772*K_1^2*x^2+9108*K_2^2*x^3+9108*K_1^2*x^3+2178*K_2^2*x^4-2178*K_1^2*x^4+28215*K_2*x^5-28215*K_1*x^5-3762*K_2^2*x^5-3762*K_1^2*x^5;
c[1]:=(2*n+5)*(n+8)*(n+1)*n*(2*n+3)*(n+3)*(n+2)*(n+9)*(540+264*n+90*K_1-90*K_2+96*n^7-576*n^3+5136*n^4-1684*n^2+864*n^6-180*K_2^2+450*K_1*K_2^2+900*K_1^2*K_2^2-180*K_1^2+3456*n^5-450*K_1^2*K_2-2700*n*K_1^2*K_2+930*n^2*K_1-900*n*K_1+720*n*K_2^2+720*n*K_1^2+2280*n^2*K_1^2+900*n*K_2-6840*n^3*K_2+60*n^4*K_1^2+450*n^2*K_1*K_2^2+2700*n*K_1*K_2^2-450*n^2*K_1^2*K_2+2280*n^2*K_2^2-930*n^2*K_2+720*n^3*K_1^2+6840*n^3*K_1+720*n^3*K_2^2+540*n^5*K_1+3270*n^4*K_1+60*n^4*K_2^2-3270*n^4*K_2-540*n^5*K_2-30*n^6*K_2+30*n^6*K_1-1350*n*K_1*K_2-8325*n^2*K_1*K_2-2700*n^3*K_1*K_2-225*n^4*K_1*K_2+4*n^8);
c[2]:=-30*(n+6)*(2*n+11)*(K_2+K_1)*(-4*n^2*K_1-24*n*K_1-2*K_1+15*K_1*K_2-n^4-12*n^3-35*n^2+6*n-3+4*n^2*K_2+24*n*K_2+2*K_2)*(2*n+5)*(n+8)*(n+1)*n*(2*n+3)*(n+3)*(n+2);
c[3]:=-3*(n+1)*n*(2*n+3)*(n+5)*(2*n+9)*(n+6)*(-12600-17340*n+7800*K_1-7800*K_2+19728*n^7+382412*n^3+483548*n^4+109612*n^2+99144*n^6-79200*K_1*K_2+10800*K_2^2+52200*K_1*K_2^2+60*n^6*K_2^2+31800*K_1^2*K_2^2+60*n^6*K_1^2+10800*K_1^2+293832*n^5-52200*K_1^2*K_2-114900*n*K_1^2*K_2+378980*n^2*K_1+118360*n*K_1+78400*n*K_2^2+78400*n*K_1^2+115920*n^2*K_1^2-118360*n*K_2-473660*n^3*K_2+13080*n^4*K_1^2+7650*n^3*K_1*K_2^2+47400*n^2*K_1*K_2^2+114900*n*K_1*K_2^2-47400*n^2*K_1^2*K_2+115920*n^2*K_2^2-378980*n^2*K_2+1420*n^5*K_1^2+57520*n^3*K_1^2+473660*n^3*K_1+57520*n^3*K_2^2-7650*n^3*K_1^2*K_2+73160*n^5*K_1+258800*n^4*K_1+13080*n^4*K_2^2-258800*n^4*K_2+1420*n^5*K_2^2-73160*n^5*K_2-11300*n^6*K_2+11300*n^6*K_1+910*n^7*K_1-910*n^7*K_2+9300*n*K_1^2*K_2^2-322800*n*K_1*K_2+900*n^2*K_1^2*K_2^2-456150*n^2*K_1*K_2-220875*n^3*K_1*K_2-450*n^4*K_1^2*K_2+450*n^4*K_1*K_2^2-49425*n^4*K_1*K_2-5325*n^5*K_1*K_2-225*n^6*K_1*K_2+30*n^8*K_1-30*n^8*K_2+148*n^9+4*n^10+2312*n^8);
c[4]:=60*(2*n+11)*(2*n+7)*(n+6)*(n+5)*(n+4)*(K_2+K_1)*(-4*n^4*K_1-56*n^3*K_1-224*n^2*K_1+15*n^2*K_1*K_2-196*n*K_1+105*n*K_1*K_2+60*K_1+90*K_1*K_2-n^6-21*n^5-154*n^4-441*n^3-313*n^2+210*n+90+4*n^4*K_2+56*n^3*K_2+224*n^2*K_2+196*n*K_2-60*K_2)*n*(2*n+3);
c[5]:=3*(n+5)*(n+4)*(2*n+11)*(n+6)*(15660*n+16200*K_1-16200*K_2+13312*n^7+188788*n^3+221692*n^4+83796*n^2+57200*n^6-54000*K_1*K_2+10800*K_2^2+27000*K_1*K_2^2+60*n^6*K_2^2+10800*K_1^2*K_2^2+60*n^6*K_1^2+10800*K_1^2+146608*n^5-27000*K_1^2*K_2-41550*n*K_1^2*K_2+193410*n^2*K_1+87930*n*K_1+38220*n*K_2^2+38220*n*K_1^2+43820*n^2*K_1^2-87930*n*K_2-206250*n^3*K_2+7480*n^4*K_1^2+4950*n^3*K_1*K_2^2+19050*n^2*K_1*K_2^2+41550*n*K_1*K_2^2-19050*n^2*K_1^2*K_2+43820*n^2*K_2^2-193410*n^2*K_2+1100*n^5*K_1^2+24520*n^3*K_1^2+206250*n^3*K_1+24520*n^3*K_2^2-4950*n^3*K_1^2*K_2+41290*n^5*K_1+121250*n^4*K_1+7480*n^4*K_2^2-121250*n^4*K_2+1100*n^5*K_2^2-41290*n^5*K_2-7870*n^6*K_2+7870*n^6*K_1+770*n^7*K_1-770*n^7*K_2+3300*n*K_1^2*K_2^2-168600*n*K_1*K_2+900*n^2*K_1^2*K_2^2-187350*n^2*K_1*K_2-97275*n^3*K_1*K_2-450*n^4*K_1^2*K_2+450*n^4*K_1*K_2^2-28425*n^4*K_1*K_2-4125*n^5*K_1*K_2-225*n^6*K_1*K_2+30*n^8*K_1-30*n^8*K_2+132*n^9+4*n^10+1808*n^8)*(2*n+5)*(n+3);
c[6]:=-30*(n+5)*(2*n+11)*(2*n+9)*(n+6)*(n+4)^2*(K_2+K_1)*(-4*n^2*K_1-32*n*K_1-30*K_1+15*K_1*K_2-n^4-16*n^3-77*n^2-104*n-45+4*n^2*K_2+32*n*K_2+30*K_2)*(2*n+3)*(n+3)*(n+2);
c[7]:=-(n+5)*(n+4)*(2*n+11)*(2*n+9)*(n+6)*(8100+38880*n+10800*K_1-10800*K_2+128*n^7+75392*n^3+39016*n^4+77052*n^2+1648*n^6-12600*K_1*K_2+3600*K_2^2+3600*K_1*K_2^2+900*K_1^2*K_2^2+3600*K_1^2+10880*n^5-3600*K_1^2*K_2-3600*n*K_1^2*K_2+46920*n^2*K_1+37440*n*K_1+7680*n*K_2^2+7680*n*K_1^2+4800*n^2*K_1^2-37440*n*K_2-25920*n^3*K_2+60*n^4*K_1^2+450*n^2*K_1*K_2^2+3600*n*K_1*K_2^2-450*n^2*K_1^2*K_2+4800*n^2*K_2^2-46920*n^2*K_2+960*n^3*K_1^2+25920*n^3*K_1+960*n^3*K_2^2+720*n^5*K_1+6420*n^4*K_1+60*n^4*K_2^2-6420*n^4*K_2-720*n^5*K_2-30*n^6*K_2+30*n^6*K_1-27000*n*K_1*K_2-17775*n^2*K_1*K_2-3600*n^3*K_1*K_2-225*n^4*K_1*K_2+4*n^8)*(n+1)*(n+3)*(n+2);
3.3 f′(1) + K1f(1) = f′(-1) + K2f(-1) = 0
In the Cartesian domain [-1,1], we provide a general formulation of
orthogonal basis functions that satisfy the generalised boundary conditions
An unnormalised basis set may be written
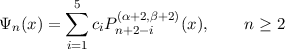
for any α > -1, β > -1 where where the ci are polynomials of degree 13 in n.
The function Ψ1 is given explicitly below. The 5 coefficients ci are determined up
to an arbitrary normalisation by imposing
- Orthogonality to Ψ1, Ψ2 and
- Two boundary conditions.
A generalised set ci for arbitrary {α,β} is currently beyond reach, but we
provide three cases with α = β = -1∕2, α = β = 1∕2 and α = β = 0
below.
Case(i) α = β = -1∕2
The ‘starting’ functions are given by
| Ψ1 | = -24 + 18K2 - 18K1 + 12K1K2 + 12xK1 + 12xK2 - 6K2x2 - 12K
1K2x2 + 6K
1x2 | |
|
| Ψ2 | = -402K1K2x3 - 168xK
1K22 + 750xK
1K2 + 168xK12K
2 - 1152x - 312K1 - 312K2 - 132K12K
2x3 - 60K
12K
2x2 + 24K
12K
2 - 120K12 + 384x3 - 255xK
22 - 255xK
12 - 174K
22x2 + 36K
12K
22x3 + 480K
1x3 - 480K
2x3 + 174K
12x2 + 201K
12x3 + 201K
22x3 - 36xK
12K
22 + 132K
1K22x3 + 120K
22 + 24K
1K22 - 1056xK
1 + 1056xK2 + 192K2x2 + 192K
1x2 - 60K
1K22x2 | | |
| c[1] | = 16(n + 3)n2(n + 4)(n + 1)(-224n + 224n2 + 656n3 - 236n4 - 576n5 + 300K
12K
2 - 15K12 + 900K
12K
22 + 800nK
1K2 + 400n2K
1K2 - 800n3K
1K2 - 450K1K2 + 440nK1 - 440nK2 - 20n2K
1 + 20n2K
2 - 800n3K
1 + 800n3K
2 - 100n4K
1 + 100n4K
2 + 360n5K
1 - 360n5K
2 - 15K22 - 300K
1K22 - 600nK
12K
2 + 600nK1K22 - 240nK
12 - 240nK
22 - 60n2K
12 - 600n2K
12K
2 + 600n2K
1K22 - 400n4K
1K2 - 60n2K
22 + 360n3K
12 + 360n3K
22 + 180n4K
12 + 180n4K
22 + 120n6K
1 - 120n6K
2 - 24n6 + 144n7 + 36n8) | |
|
| c[2] | = -480(n + 3)n2(2n + 5)(2n + 1)(n + 2)(-2n4 - 4n3 - 6n2K
1 + 6n2K
2 + 6n2 - 6nK
1 + 6nK2 + 8n + 10K1K2 + 7K1 - 7K2 - 8)(K1 + K2) | |
|
| c[3] | = -8(2n + 5)(2n + 3)(-960n + 256n2 + 3840n3 + 1000n4 - 4200n5 - 1800K
12K
2 + 450K12 + 1800K
12K
22 - 2100nK
1K2 - 2650n2K
1K2 - 4800n3K
1K2 - 900K1K2 + 240nK1 - 240nK2 + 2120n2K
1 - 2120n2K
2 - 720n3K
1 + 720n3K
2 - 1660n4K
1 + 1660n4K
2 + 1800n5K
1 - 1800n5K
2 + 450K22 + 1800K
1K22 + 1800nK
12K
22 - 1800nK
12K
2 + 1800nK1K22 + 1530nK
12 + 1530nK
22 - 915n2K
12 + 900n2K
12K
22 - 3300n2K
12K
2 + 3300n2K
1K22 - 2400n3K
12K
2 + 2400n3K
1K22 - 600n4K
12K
2 + 600n4K
1K22 - 5200n4K
1K2 - 2400n5K
1K2 - 915n2K
22 - 240n3K
12 - 240n3K
22 + 1740n4K
12 + 1740n4K
22 + 1080n5K
12 + 180n6K
12 + 2540n6K
1 + 180n6K
22 - 2540n6K
2 + 960n7K
1 - 960n7K
2 + 120n8K
1 - 120n8K
2 + 1080n5K
22 - 2492n6 + 960n7 + 1200n8 + 360n9 - 400n6K
1K2 + 36n10)(n + 1) | |
|
| c[4] | = 120n(2n + 5)(2n + 1)(n + 2)(2n + 3)2(K
1 + K2)(-6n2K
1 - 18nK1 - 5K1 + 10K1K2 - 2n4 - 12n3 - 18n2 + 6n2K
2 + 18nK2 + 5K2) | |
|
| c[5] | = (2n + 5)(2n + 3)(2n + 1)(2n - 1)(n + 2)(-480n - 1312n2 + 528n3 + 4084n4 + 4320n5 - 900K
12K
2 + 225K12 + 900K
12K
22 - 2400nK
1K2 - 4400n2K
1K2 - 2400n3K
1K2 - 450K1K2 + 120nK1 - 120nK2 + 2380n2K
1 - 2380n2K
2 + 4800n3K
1 - 4800n3K
2 + 3500n4K
1 - 3500n4K
2 + 1080n5K
1 - 1080n5K
2 + 225K22 + 900K
1K22 - 1800nK
12K
2 + 1800nK1K22 + 1440nK
12 + 1440nK
22 + 2100n2K
12 - 600n2K
12K
2 + 600n2K
1K22 - 400n4K
1K2 + 2100n2K
22 + 1080n3K
12 + 1080n3K
22 + 180n4K
12 + 180n4K
22 + 120n6K
1 - 120n6K
2 + 1992n6 + 432n7 + 36n8) | | |
Expressions for all quantities involved are provided below.
Psi_1:=-24+18*K_2-18*K_1+12*K_1*K_2+12*x*K_1+12*x*K_2-6*K_2*x^2-12*K_1*K_2*x^2+6*K_1*x^2;
Psi_2:=750*x*K_1*K_2-60*K_1^2*K_2*x^2-168*x*K_1*K_2^2-1152*x-60*K_1*K_2^2*x^2+168*x*K_1^2*K_2-312*K_1-312*K_2+132*K_1*K_2^2*x^3-402*K_1*K_2*x^3+36*K_1^2*K_2^2*x^3-132*K_1^2*K_2*x^3-36*x*K_1^2*K_2^2+384*x^3+24*K_1^2*K_2-120*K_1^2+192*K_1*x^2+192*K_2*x^2-1056*x*K_1+1056*x*K_2+201*K_2^2*x^3+201*K_1^2*x^3-480*K_2*x^3+480*K_1*x^3+174*K_1^2*x^2-174*K_2^2*x^2-255*x*K_1^2-255*x*K_2^2+120*K_2^2+24*K_1*K_2^2;
c[1]:=16*(n+3)*n^2*(n+4)*(n+1)*(-224*n+224*n^2+656*n^3-236*n^4-576*n^5+300*K_1^2*K_2-15*K_1^2+900*K_1^2*K_2^2+800*n*K_1*K_2+400*n^2*K_1*K_2-800*n^3*K_1*K_2-450*K_1*K_2+440*n*K_1-440*n*K_2-20*n^2*K_1+20*n^2*K_2-800*n^3*K_1+800*n^3*K_2-100*n^4*K_1+100*n^4*K_2+360*n^5*K_1-360*n^5*K_2-15*K_2^2-300*K_1*K_2^2-600*n*K_1^2*K_2+600*n*K_1*K_2^2-240*n*K_1^2-240*n*K_2^2-60*n^2*K_1^2-600*n^2*K_1^2*K_2+600*n^2*K_1*K_2^2-400*n^4*K_1*K_2-60*n^2*K_2^2+360*n^3*K_1^2+360*n^3*K_2^2+180*n^4*K_1^2+180*n^4*K_2^2+120*n^6*K_1-120*n^6*K_2-24*n^6+144*n^7+36*n^8);
c[2]:=-480*(n+3)*n^2*(2*n+5)*(2*n+1)*(n+2)*(-2*n^4-4*n^3-6*n^2*K_1+6*n^2*K_2+6*n^2-6*n*K_1+6*n*K_2+8*n+10*K_1*K_2+7*K_1-7*K_2-8)*(K_1+K_2);
c[3]:=-8*(2*n+5)*(2*n+3)*(-960*n+256*n^2+3840*n^3+1000*n^4-4200*n^5-1800*K_1^2*K_2+450*K_1^2+1800*K_1^2*K_2^2-2100*n*K_1*K_2-2650*n^2*K_1*K_2-4800*n^3*K_1*K_2-900*K_1*K_2+240*n*K_1-240*n*K_2+2120*n^2*K_1-2120*n^2*K_2-720*n^3*K_1+720*n^3*K_2-1660*n^4*K_1+1660*n^4*K_2+1800*n^5*K_1-1800*n^5*K_2+450*K_2^2+1800*K_1*K_2^2+1800*n*K_1^2*K_2^2-1800*n*K_1^2*K_2+1800*n*K_1*K_2^2+1530*n*K_1^2+1530*n*K_2^2-915*n^2*K_1^2+900*n^2*K_1^2*K_2^2-3300*n^2*K_1^2*K_2+3300*n^2*K_1*K_2^2-2400*n^3*K_1^2*K_2+2400*n^3*K_1*K_2^2-600*n^4*K_1^2*K_2+600*n^4*K_1*K_2^2-5200*n^4*K_1*K_2-2400*n^5*K_1*K_2-915*n^2*K_2^2-240*n^3*K_1^2-240*n^3*K_2^2+1740*n^4*K_1^2+1740*n^4*K_2^2+1080*n^5*K_1^2+180*n^6*K_1^2+2540*n^6*K_1+180*n^6*K_2^2-2540*n^6*K_2+960*n^7*K_1-960*n^7*K_2+120*n^8*K_1-120*n^8*K_2+1080*n^5*K_2^2-2492*n^6+960*n^7+1200*n^8+360*n^9-400*n^6*K_1*K_2+36*n^10)*(n+1);
c[4]:=120*n*(2*n+5)*(2*n+1)*(n+2)*(2*n+3)^2*(K_1+K_2)*(-6*n^2*K_1-18*n*K_1-5*K_1+10*K_1*K_2-2*n^4-12*n^3-18*n^2+6*n^2*K_2+18*n*K_2+5*K_2);
c[5]:=(2*n+5)*(2*n+3)*(2*n+1)*(2*n-1)*(n+2)*(-480*n-1312*n^2+528*n^3+4084*n^4+4320*n^5-900*K_1^2*K_2+225*K_1^2+900*K_1^2*K_2^2-2400*n*K_1*K_2-4400*n^2*K_1*K_2-2400*n^3*K_1*K_2-450*K_1*K_2+120*n*K_1-120*n*K_2+2380*n^2*K_1-2380*n^2*K_2+4800*n^3*K_1-4800*n^3*K_2+3500*n^4*K_1-3500*n^4*K_2+1080*n^5*K_1-1080*n^5*K_2+225*K_2^2+900*K_1*K_2^2-1800*n*K_1^2*K_2+1800*n*K_1*K_2^2+1440*n*K_1^2+1440*n*K_2^2+2100*n^2*K_1^2-600*n^2*K_1^2*K_2+600*n^2*K_1*K_2^2-400*n^4*K_1*K_2+2100*n^2*K_2^2+1080*n^3*K_1^2+1080*n^3*K_2^2+180*n^4*K_1^2+180*n^4*K_2^2+120*n^6*K_1-120*n^6*K_2+1992*n^6+432*n^7+36*n^8);
Case(ii) α = β = 1∕2
The ‘starting’ functions are given by
| Ψ1 | = -32 + 24K2 - 24K1 + 16K1K2 + 16xK2 + 16xK1 + 8K1x2 - 16K
1K2x2 - 8K
2x2 | |
|
| Ψ2 | = -224K2 - 1536x - 224K1 + 1600xK2 - 1600xK1 + 256K1x2 + 256K
2x2 - 808K
1K2x3 + 272K
1K22x3 - 272K
12K
2x3 + 80K
12K
22x3 - 112K
1K22x2 - 112K
12K
2x2 - 352xK
1K22 + 352xK
12K
2 + 1496xK1K2 - 80xK12K
22 + 512x3 - 96K
12 + 32K
12K
2 - 396xK22 + 96K
22 + 32K
1K22 - 396xK
12 - 216K
22x2 + 216K
12x2 - 704K
2x3 + 704K
1x3 + 276K
12x3 + 276K
22x3 | | |
| c[1] | = 16(n + 5)(n + 1)2n(n + 6)(-3648n - 10656n3 - 15276n4 + 21680n2 + 2160n5 + 4440n6 + 1200n7 + 100n8 + 44100K
12K
22 + 945K
12 + 26460K
12K
2 + 945K22 - 26460K
1K22 - 22050K
1K2 - 52920nK12K
2 + 52920nK1K22 - 17640nK
12 + 23184nK
1 - 17640nK22 - 23184nK
2 - 17640n2K
12K
2 + 17640n2K
1K22 + 13020n2K
12 - 39900n2K
1 + 13020n2K
22 + 39900n2K
2 + 12600n3K
12 - 9072n3K
1 + 12600n3K
22 + 9072n3K
2 + 2100n4K
12 + 17388n4K
1 + 2100n4K
22 - 17388n4K
2 + 7560n5K
1 - 7560n5K
2 - 840n6K
2 + 840n6K
1 + 84672nK1K2 - 35280n2K
1K2 - 42336n3K
1K2 - 7056n4K
1K2) | |
|
| c[2] | = -3360(n + 5)(n + 1)n(2n + 3)(n + 3)(2n + 7)(K2 + K1)(-10n2K
1 - 30nK1 + 42K1K2 + 19K1 - 2n4 - 12n3 - 6n2 + 36n - 16 + 10n2K
2 + 30nK2 - 19K2) | |
|
| c[3] | = -8(2n + 5)(n + 2)(2n + 7)(20160n + 2100n6K
12 - 196448n3 + 2100n6K
22 + 840n8K
1 - 840n8K
2 - 7056n6K
1K2 - 89356n4 - 65808n2 + 108048n5 + 138924n6 + 66240n7 + 16140n8 + 2000n9 + 100n10 + 396900K
12K
22 - 33075K
12 - 132300K
12K
2 - 33075K22 + 132300K
1K22 + 66150K
1K2 - 599760nK12K
2 + 599760nK1K22 + 3780nK
12 - 126000nK
1 + 3780nK22 + 126000nK
2 - 432180n2K
12K
2 + 432180n2K
1K22 - 141120n3K
12K
2 + 141120n3K
1K22 + 175665n2K
12 - 130956n2K
1 + 175665n2K
22 + 130956n2K
2 + 221760n3K
12 + 202944n3K
1 + 221760n3K
22 - 202944n3K
2 + 111720n4K
12 + 398328n4K
1 + 111720n4K
22 - 398328n4K
2 + 25200n5K
12 + 262416n5K
1 + 25200n5K
22 - 262416n5K
2 - 84588n6K
2 + 84588n6K
1 + 13440n7K
1 - 13440n7K
2 + 176400nK12K
22 - 158760nK
1K2 + 44100n2K
12K
22 - 942858n2K
1K2 - 903168n3K
1K2 - 17640n4K
12K
2 + 17640n4K
1K22 - 395136n4K
1K2 - 84672n5K
1K2) | |
|
| c[4] | = 840(2n + 3)(n + 3)(2n + 7)(2n + 5)2(K
2 + K1)(-10n2K
1 - 50nK1 - 21K1 + 42K1K2 - 2n4 - 20n3 - 54n2 - 20n + 10n2K
2 + 50nK2 + 21K2)(n + 1) | |
|
| c[5] | = (2n + 7)(2n + 5)(2n + 3)(2n + 1)(n + 3)(-6720n + 86240n3 + 111124n4 + 14256n2 + 59600n5 + 15640n6 + 2000n7 + 100n8 + 44100K
12K
22 + 11025K
12 - 44100K
12K
2 + 11025K22 + 44100K
1K22 - 22050K
1K2 - 88200nK12K
2 + 88200nK1K22 + 54600nK
12 + 28560nK
1 + 54600nK22 - 28560nK
2 - 17640n2K
12K
2 + 17640n2K
1K22 + 63420n2K
12 + 125412n2K
1 + 63420n2K
22 - 125412n2K
2 + 21000n3K
12 + 152880n3K
1 + 21000n3K
22 - 152880n3K
2 + 2100n4K
12 + 67788n4K
1 + 2100n4K
22 - 67788n4K
2 + 12600n5K
1 - 12600n5K
2 - 840n6K
2 + 840n6K
1 - 141120nK1K2 - 204624n2K
1K2 - 70560n3K
1K2 - 7056n4K
1K2) | | |
Expressions for all quantities involved are provided below.
Psi_1:=-32+24*K_2-24*K_1+16*K_1*K_2+16*x*K_2+16*x*K_1+8*K_1*x^2-16*K_1*K_2*x^2-8*K_2*x^2;
Psi_2:=-224*K_2-1536*x-224*K_1+1600*x*K_2-1600*x*K_1+256*K_1*x^2+256*K_2*x^2-808*K_1*K_2*x^3+272*K_1*K_2^2*x^3-272*K_1^2*K_2*x^3+80*K_1^2*K_2^2*x^3-112*K_1*K_2^2*x^2-112*K_1^2*K_2*x^2-352*x*K_1*K_2^2+352*x*K_1^2*K_2+1496*x*K_1*K_2-80*x*K_1^2*K_2^2+512*x^3-96*K_1^2+32*K_1^2*K_2-396*x*K_2^2+96*K_2^2+32*K_1*K_2^2-396*x*K_1^2-216*K_2^2*x^2+216*K_1^2*x^2-704*K_2*x^3+704*K_1*x^3+276*K_1^2*x^3+276*K_2^2*x^3;
c[1]:=16*(n+5)*(n+1)^2*n*(n+6)*(-3648*n-10656*n^3-15276*n^4+21680*n^2+2160*n^5+4440*n^6+1200*n^7+100*n^8+44100*K_1^2*K_2^2+945*K_1^2+26460*K_1^2*K_2+945*K_2^2-26460*K_1*K_2^2-22050*K_1*K_2-52920*n*K_1^2*K_2+52920*n*K_1*K_2^2-17640*n*K_1^2+23184*n*K_1-17640*n*K_2^2-23184*n*K_2-17640*n^2*K_1^2*K_2+17640*n^2*K_1*K_2^2+13020*n^2*K_1^2-39900*n^2*K_1+13020*n^2*K_2^2+39900*n^2*K_2+12600*n^3*K_1^2-9072*n^3*K_1+12600*n^3*K_2^2+9072*n^3*K_2+2100*n^4*K_1^2+17388*n^4*K_1+2100*n^4*K_2^2-17388*n^4*K_2+7560*n^5*K_1-7560*n^5*K_2-840*n^6*K_2+840*n^6*K_1+84672*n*K_1*K_2-35280*n^2*K_1*K_2-42336*n^3*K_1*K_2-7056*n^4*K_1*K_2);
c[2]:=-3360*(n+5)*(n+1)*n*(2*n+3)*(n+3)*(2*n+7)*(K_2+K_1)*(-10*n^2*K_1-30*n*K_1+42*K_1*K_2+19*K_1-2*n^4-12*n^3-6*n^2+36*n-16+10*n^2*K_2+30*n*K_2-19*K_2);
c[3]:=-8*(2*n+5)*(n+2)*(2*n+7)*(20160*n+2100*n^6*K_1^2-196448*n^3+2100*n^6*K_2^2+840*n^8*K_1-840*n^8*K_2-7056*n^6*K_1*K_2-89356*n^4-65808*n^2+108048*n^5+138924*n^6+66240*n^7+16140*n^8+2000*n^9+100*n^10+396900*K_1^2*K_2^2-33075*K_1^2-132300*K_1^2*K_2-33075*K_2^2+132300*K_1*K_2^2+66150*K_1*K_2-599760*n*K_1^2*K_2+599760*n*K_1*K_2^2+3780*n*K_1^2-126000*n*K_1+3780*n*K_2^2+126000*n*K_2-432180*n^2*K_1^2*K_2+432180*n^2*K_1*K_2^2-141120*n^3*K_1^2*K_2+141120*n^3*K_1*K_2^2+175665*n^2*K_1^2-130956*n^2*K_1+175665*n^2*K_2^2+130956*n^2*K_2+221760*n^3*K_1^2+202944*n^3*K_1+221760*n^3*K_2^2-202944*n^3*K_2+111720*n^4*K_1^2+398328*n^4*K_1+111720*n^4*K_2^2-398328*n^4*K_2+25200*n^5*K_1^2+262416*n^5*K_1+25200*n^5*K_2^2-262416*n^5*K_2-84588*n^6*K_2+84588*n^6*K_1+13440*n^7*K_1-13440*n^7*K_2+176400*n*K_1^2*K_2^2-158760*n*K_1*K_2+44100*n^2*K_1^2*K_2^2-942858*n^2*K_1*K_2-903168*n^3*K_1*K_2-17640*n^4*K_1^2*K_2+17640*n^4*K_1*K_2^2-395136*n^4*K_1*K_2-84672*n^5*K_1*K_2);
c[4]:=840*(2*n+3)*(n+3)*(2*n+7)*(2*n+5)^2*(K_2+K_1)*(-10*n^2*K_1-50*n*K_1-21*K_1+42*K_1*K_2-2*n^4-20*n^3-54*n^2-20*n+10*n^2*K_2+50*n*K_2+21*K_2)*(n+1);
c[5]:=(2*n+7)*(2*n+5)*(2*n+3)*(2*n+1)*(n+3)*(-6720*n+86240*n^3+111124*n^4+14256*n^2+59600*n^5+15640*n^6+2000*n^7+100*n^8+44100*K_1^2*K_2^2+11025*K_1^2-44100*K_1^2*K_2+11025*K_2^2+44100*K_1*K_2^2-22050*K_1*K_2-88200*n*K_1^2*K_2+88200*n*K_1*K_2^2+54600*n*K_1^2+28560*n*K_1+54600*n*K_2^2-28560*n*K_2-17640*n^2*K_1^2*K_2+17640*n^2*K_1*K_2^2+63420*n^2*K_1^2+125412*n^2*K_1+63420*n^2*K_2^2-125412*n^2*K_2+21000*n^3*K_1^2+152880*n^3*K_1+21000*n^3*K_2^2-152880*n^3*K_2+2100*n^4*K_1^2+67788*n^4*K_1+2100*n^4*K_2^2-67788*n^4*K_2+12600*n^5*K_1-12600*n^5*K_2-840*n^6*K_2+840*n^6*K_1-141120*n*K_1*K_2-204624*n^2*K_1*K_2-70560*n^3*K_1*K_2-7056*n^4*K_1*K_2);
Case(iii) α = β = 0
The ‘starting’ functions are given by
| Ψ1 | = -28 + 21K2 - 21K1 + 14K1K2 + 14xK2 + 14xK1 + 7K1x2 - 14K
1K2x2 - 7K
2x2 | |
|
| Ψ2 | = -126xK1K22 - 630x + 546xK
1K2 - 119K1 - 119K2 + 98K1K22x3 + 28K
12K
22x3 - 98K
12K
2x3 - 294K
1K2x3 - 42K
12K
2x2 - 42K
1K22x2 + 126xK
12K
2 + 630xK2 - 630xK1 + 105K1x2 + 105K
2x2 + 210x3 - 154xK
22 - 154xK
12 - 91K
22x2 + 91K
12x2 + 14K
12K
2 - 49K12 + 280K
1x3 - 280K
2x3 + 112K
12x3 + 112K
22x3 - 28xK
12K
22 + 49K
22 + 14K
1K22 | | |
| c[1] | = (n + 5)(-18n + 16n6 + 8n7 + 63n2 - 62n4 - 16n5 + 8n3 + 72K
12K
2 + 144K12K
22 + 144nK
1K22 - 72n2K
12K
2 + 72n2K
1K22 + 216nK
2K1 - 36n2K
2K1 - 144nK12K
2 - 144n3K
2K1 - 36n4K
2K1 - 72K1K2 - 48nK12 - 72K
1K22 + 36n5K
1 + 6n6K
1 - 6n6K
2 + 12n4K
12 + 42n4K
1 + 12n4K
22 + 72nK
1 - 48nK22 - 72nK
2 - 42n4K
2 - 36n5K
2 + 24n2K
12 - 84n2K
1 + 24n2K
22 + 84n2K
2 + 48n3K
12 - 72n3K
1 + 48n3K
22 + 72n3K
2 + n8)(n + 1)(1 + 2n)n(n + 4) | |
|
| c[2] | = -6(n + 1)(1 + 2n)n(n + 4)(n + 3)(2n + 5)(K2 + K1)(12K1K2 - 4n2K
1 + 6K1 - 8nK1 - n4 - 4n3 + n2 + 10n - 6 + 4n2K
2 - 6K2 + 8nK2) | |
|
| c[3] | = -2(2n + 3)(n + 3)(n + 2)(237n6 + 234n7 + 72n2 - 397n4 - 135n5 - 114n3 - 360K
12K
2 + 720K12K
22 + 144n2K
12K
22 + 12n6K
12 + 12n6K
22 - 72n4K
12K
2 + 72n4K
1K22 + 6n8K
1 - 36n6K
1K2 - 6n8K
2 + 972nK1K22 - 972n2K
12K
2 + 972n2K
1K22 - 432nK
2K1 + 432nK12K
22 + 432n3K
1K22 - 432n3K
12K
2 - 1440n2K
2K1 - 972nK12K
2 - 324n5K
2K1 - 1836n3K
2K1 - 1116n4K
2K1 + 90nK12 + 360K
1K22 + n10 + 675n5K
1 + 327n6K
1 - 327n6K
2 + 336n4K
12 + 561n4K
1 + 336n4K
22 - 90nK
1 + 90nK22 + 90nK
2 - 561n4K
2 - 675n5K
2 + 138n2K
12 - 84n2K
1 + 138n2K
22 + 84n2K
2 + 396n3K
12 + 45n3K
1 + 396n3K
22 - 45n3K
2 + 87n8 + 15n9 + 108n5K
12 + 108n5K
22 + 72n7K
1 - 72n7K
2) | |
|
| c[4] | = 6(n + 1)(1 + 2n)(n + 3)(2n + 5)(n + 2)2(K
2 + K1)(-4n2K
1 - 16nK1 - 6K1 + 12K1K2 - n4 - 8n3 - 17n2 - 4n + 4n2K
2 + 16nK2 + 6K2) | |
|
| c[5] | = (n + 1)n(2n + 5)(n + 3)(n + 2)(-36n + 100n6 + 16n7 - 9n2 + 448n4 + 304n5 + 256n3 - 144K
12K
2 + 36K12 + 144K
12K
22 + 288nK
1K22 - 72n2K
12K
2 + 72n2K
1K22 - 432nK
2K1 - 684n2K
2K1 - 288nK12K
2 - 288n3K
2K1 - 36n4K
2K1 - 72K1K2 + 192nK12 + 36K
22 + 144K
1K22 + 72n5K
1 + 6n6K
1 - 6n6K
2 + 12n4K
12 + 312n4K
1 + 12n4K
22 + 72nK
1 + 192nK22 - 72nK
2 - 312n4K
2 - 72n5K
2 + 240n2K
12 + 402n2K
1 + 240n2K
22 - 402n2K
2 + 96n3K
12 + 576n3K
1 + 96n3K
22 - 576n3K
2 + n8) | | |
Expressions for all quantities involved are provided below.
Psi_1:=-28+21*K_2-21*K_1+14*K_1*K_2+14*x*K_2+14*x*K_1+7*K_1*x^2-14*K_1*K_2*x^2-7*K_2*x^2;
Psi_2:=-630*x-42*K_1^2*K_2*x^2-42*K_1*K_2^2*x^2+126*x*K_1^2*K_2+546*x*K_1*K_2-126*x*K_1*K_2^2-28*x*K_1^2*K_2^2-119*K_1-119*K_2+98*K_1*K_2^2*x^3-294*K_1*K_2*x^3+28*K_1^2*K_2^2*x^3-98*K_1^2*K_2*x^3+105*K_2*x^2+105*K_1*x^2-630*x*K_1+630*x*K_2+14*K_1^2*K_2-49*K_1^2-154*x*K_1^2-154*x*K_2^2+91*K_1^2*x^2-91*K_2^2*x^2-280*K_2*x^3+280*K_1*x^3+112*K_2^2*x^3+112*K_1^2*x^3+210*x^3+49*K_2^2+14*K_1*K_2^2;
c[1]:=(n+5)*(-18*n+16*n^6+8*n^7+63*n^2-62*n^4-16*n^5+8*n^3+72*K_1^2*K_2+144*K_1^2*K_2^2+144*n*K_1*K_2^2-72*n^2*K_1^2*K_2+72*n^2*K_1*K_2^2+216*n*K_2*K_1-36*n^2*K_2*K_1-144*n*K_1^2*K_2-144*n^3*K_2*K_1-36*n^4*K_2*K_1-72*K_1*K_2-48*n*K_1^2-72*K_1*K_2^2+36*n^5*K_1+6*n^6*K_1-6*n^6*K_2+12*n^4*K_1^2+42*n^4*K_1+12*n^4*K_2^2+72*n*K_1-48*n*K_2^2-72*n*K_2-42*n^4*K_2-36*n^5*K_2+24*n^2*K_1^2-84*n^2*K_1+24*n^2*K_2^2+84*n^2*K_2+48*n^3*K_1^2-72*n^3*K_1+48*n^3*K_2^2+72*n^3*K_2+n^8)*(n+1)*(1+2*n)*n*(n+4);
c[2]:=-6*(n+1)*(1+2*n)*n*(n+4)*(n+3)*(2*n+5)*(K_2+K_1)*(12*K_1*K_2-4*n^2*K_1+6*K_1-8*n*K_1-n^4-4*n^3+n^2+10*n-6+4*n^2*K_2-6*K_2+8*n*K_2);
c[3]:=-2*(2*n+3)*(n+3)*(n+2)*(237*n^6+234*n^7+72*n^2-397*n^4-135*n^5-114*n^3-360*K_1^2*K_2+720*K_1^2*K_2^2+144*n^2*K_1^2*K_2^2+12*n^6*K_1^2+12*n^6*K_2^2-72*n^4*K_1^2*K_2+72*n^4*K_1*K_2^2+6*n^8*K_1-36*n^6*K_1*K_2-6*n^8*K_2+972*n*K_1*K_2^2-972*n^2*K_1^2*K_2+972*n^2*K_1*K_2^2-432*n*K_2*K_1+432*n*K_1^2*K_2^2+432*n^3*K_1*K_2^2-432*n^3*K_1^2*K_2-1440*n^2*K_2*K_1-972*n*K_1^2*K_2-324*n^5*K_2*K_1-1836*n^3*K_2*K_1-1116*n^4*K_2*K_1+90*n*K_1^2+360*K_1*K_2^2+n^10+675*n^5*K_1+327*n^6*K_1-327*n^6*K_2+336*n^4*K_1^2+561*n^4*K_1+336*n^4*K_2^2-90*n*K_1+90*n*K_2^2+90*n*K_2-561*n^4*K_2-675*n^5*K_2+138*n^2*K_1^2-84*n^2*K_1+138*n^2*K_2^2+84*n^2*K_2+396*n^3*K_1^2+45*n^3*K_1+396*n^3*K_2^2-45*n^3*K_2+87*n^8+15*n^9+108*n^5*K_1^2+108*n^5*K_2^2+72*n^7*K_1-72*n^7*K_2);
c[4]:=6*(n+1)*(1+2*n)*(n+3)*(2*n+5)*(n+2)^2*(K_2+K_1)*(-4*n^2*K_1-16*n*K_1-6*K_1+12*K_1*K_2-n^4-8*n^3-17*n^2-4*n+4*n^2*K_2+16*n*K_2+6*K_2);
c[5]:=(n+1)*n*(2*n+5)*(n+3)*(n+2)*(-36*n+100*n^6+16*n^7-9*n^2+448*n^4+304*n^5+256*n^3-144*K_1^2*K_2+36*K_1^2+144*K_1^2*K_2^2+288*n*K_1*K_2^2-72*n^2*K_1^2*K_2+72*n^2*K_1*K_2^2-432*n*K_2*K_1-684*n^2*K_2*K_1-288*n*K_1^2*K_2-288*n^3*K_2*K_1-36*n^4*K_2*K_1-72*K_1*K_2+192*n*K_1^2+36*K_2^2+144*K_1*K_2^2+72*n^5*K_1+6*n^6*K_1-6*n^6*K_2+12*n^4*K_1^2+312*n^4*K_1+12*n^4*K_2^2+72*n*K_1+192*n*K_2^2-72*n*K_2-312*n^4*K_2-72*n^5*K_2+240*n^2*K_1^2+402*n^2*K_1+240*n^2*K_2^2-402*n^2*K_2+96*n^3*K_1^2+576*n^3*K_1+96*n^3*K_2^2-576*n^3*K_2+n^8);