6. Gaussian Plumes from High Chimneys
The Gaussian plume equation (47) assumed that the source was at
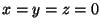 . We can easily change this so that the source is from a chimney
of height
. We can easily change this so that the source is from a chimney
of height 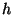 by replacing Eq. (47) by
by replacing Eq. (47) by
However, this equation tells us that diffusion takes place not only for
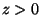 (above the ground) but also for
(above the ground) but also for 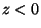 (below the ground). The simplest
assumption available to correct this is to assume that any pollutant which
reaches the ground is reflected back. Thus the pollutant which, according to
Eq. (58) should be below the ground actually appears above the ground. This
is exactly equivalent to allowing Eq. (58) to apply unmodified but then
introducing another source at
(below the ground). The simplest
assumption available to correct this is to assume that any pollutant which
reaches the ground is reflected back. Thus the pollutant which, according to
Eq. (58) should be below the ground actually appears above the ground. This
is exactly equivalent to allowing Eq. (58) to apply unmodified but then
introducing another source at 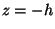 (i.e. the image of the true source in
the ground). We then replace Eq. (58) by
(i.e. the image of the true source in
the ground). We then replace Eq. (58) by
and use Eq. (59) for 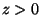 only. The concentration at ground level is
only. The concentration at ground level is
Fig. 12 shows the concentration at ground level downwind of two chimneys
(one 25 m high and the other 50 m high) emitting the same amount of
pollutant. It is clear that for the higher chimney the maximum concentration
is both lower and further down wind.
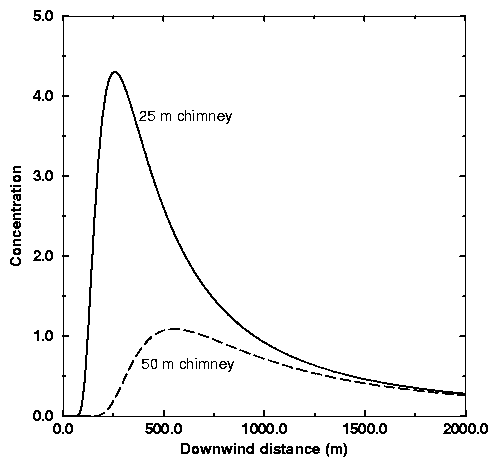
Fig. 12. The ground level concentration of pollutant
down wind of two chimneys emitting equal amounts of pollutant. Pasquill
stability class C is assumed.
If we consider the Pasquill-Gifford stability class C (slightly unstable)
then
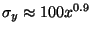 and
and
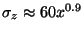 . The
maximum ground level concentration according to Eq. (60) can then be shown to
be at
. The
maximum ground level concentration according to Eq. (60) can then be shown to
be at
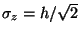 and its value is
and its value is
Note that the maximum concentration decreases as the square of the
chimney height -- so tall chimneys are a good idea.
back to syllabus
![\begin{displaymath}
C(x,y,z)={q\over 2\pi\sigma_y\sigma_zu}\left [{\rm exp}\left...
...ma_y^2}-{(z+h)^2\over 2\sigma_z^2}\right )
\right ]\eqno{(59)}
\end{displaymath}](img230.png)

![]() and
and
![]() . The
maximum ground level concentration according to Eq. (60) can then be shown to
be at
. The
maximum ground level concentration according to Eq. (60) can then be shown to
be at
![]() and its value is
and its value is