The arithmetic operator which allows the user to define arithmetic formulas based on fields and constants which are then executed BDMAS style. This works by parsing the text forumula into an execution tree which is walked in order to perform the final result. Building the tree is the potentially expensive aspect of this, so built trees are cached as it is likely that the equation will be run many times. Currently this is expressed in terms of scalars, and it will operate on all elements of the data. More...
Data Types | |
| type | arithmetic_cache_item |
| type | arithmetic_execution_node |
Functions/Subroutines | |
| subroutine, public | initialise_arithmetic_operator () |
| Initialises this operator. More... | |
| subroutine, public | finalise_arithmetic_operator () |
| Finalises this opertor. More... | |
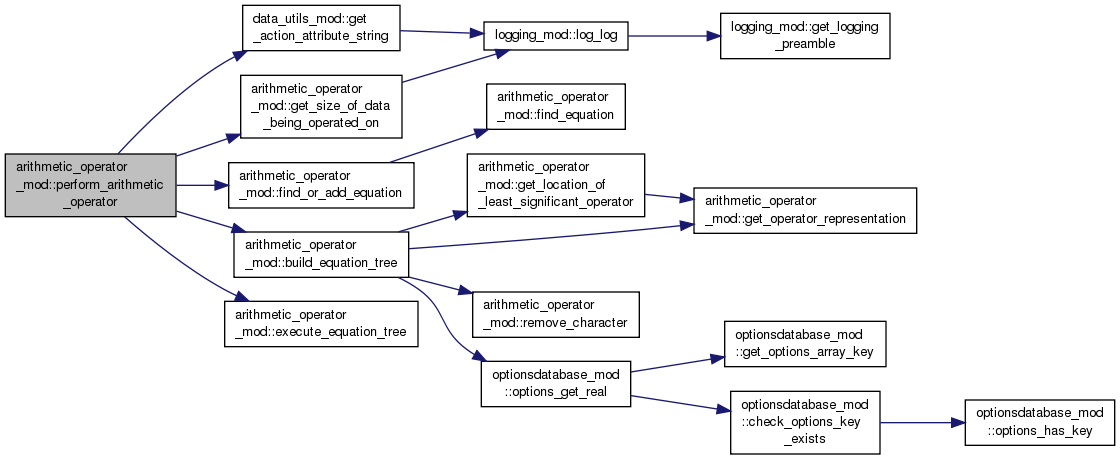
| subroutine, public | perform_arithmetic_operator (io_configuration, field_values, action_attributes, source_monc_location, source_monc, operator_result_values) |
| Executes this arithmetic operator by attempting to retrieved the cached equation (and creates one if not found.) If there is no execution tree it then parses the equation into an execution tree and stores it. The stored execution tree is then executed and the real result returned. More... | |
| integer function | get_size_of_data_being_operated_on (cached_equation, field_values) |
| Retrieves the number of data elements that this will operate on. It will produce a log error if any variable lengths are inconsistent. More... | |
| recursive real(kind=default_precision) function, dimension(n) | execute_equation_tree (equation_tree, field_values, n) |
| Executes an equation tree by doing a post order traversal of the tree. If a node is a terminal then either the variable is looked up for its value or the constant is returned. If a node is a non terminal then the operator is performed on the result value of its left and right subtrees and the value returned. More... | |
| recursive type(arithmetic_execution_node) function, pointer | build_equation_tree (io_configuration, equation) |
| Builds the equation tree, this searches for the least significant operator and then splits the equation based upon that. Each sub equation is then passed to recursive calls of this function which return subtrees for these aspects. Some string manipulation is done to remove braces which would otherwise be included in the terminal characters. More... | |
| subroutine | remove_character (raw_string, c) |
| Removes all occurances of a character from a string in situ by replacing it with whitespace. More... | |
| integer function | get_location_of_least_significant_operator (equation) |
| Given an equation this will retrieve the location of the least significant operator in that equation or 0 if no operator is found (i.e. the string is a terminal.) This takes account of parenthesis. More... | |
| integer function | get_operator_representation (op_char) |
| Given a character representation of an operator this returns the internal numeric type representation of it. More... | |
| type(list_type) function, public | arithmetic_operator_get_required_fields (action_attributes) |
| Retrieves the list of fields needed by this operator for a specific configuration. More... | |
| type(list_type) function | process_equation_to_get_required_fields (equation) |
| Performs text processing on an equation to extract out all the required variable (fields) needed in order to run this equation and get the result. Note this ignores all values which are constants (reals or integers) More... | |
| type(arithmetic_cache_item) function, pointer | find_or_add_equation (equation) |
| Locates an existing equation in the cache based upon the textual equation representation or creates a new entry and returns this one. More... | |
| type(arithmetic_cache_item) function, pointer | find_equation (equation, dolock) |
| Finds an equation in the cache based upon its textual equation representation or returns null if none is found. More... | |
Variables | |
| integer, parameter | terminal_op =0 |
| integer, parameter | add_op =1 |
| integer, parameter | minus_op =2 |
| integer, parameter | mul_op =3 |
| integer, parameter | div_op =4 |
| integer, parameter | mod_op =5 |
| A specific node in the execution tree. More... | |
| type(hashmap_type), volatile | equation_cache |
| integer, volatile | equation_cache_rwlock |
Detailed Description
The arithmetic operator which allows the user to define arithmetic formulas based on fields and constants which are then executed BDMAS style. This works by parsing the text forumula into an execution tree which is walked in order to perform the final result. Building the tree is the potentially expensive aspect of this, so built trees are cached as it is likely that the equation will be run many times. Currently this is expressed in terms of scalars, and it will operate on all elements of the data.
Function/Subroutine Documentation
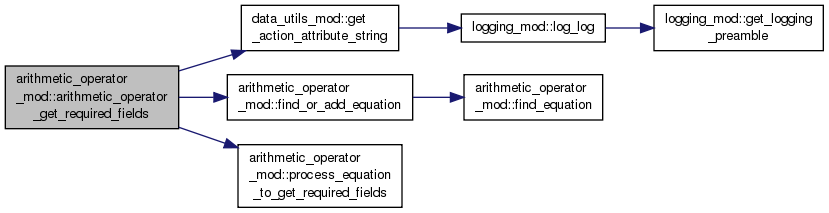
◆ arithmetic_operator_get_required_fields()
| type(list_type) function, public arithmetic_operator_mod::arithmetic_operator_get_required_fields | ( | type(map_type), intent(inout) | action_attributes | ) |
Retrieves the list of fields needed by this operator for a specific configuration.
- Parameters
-
action_attributes The attributes which configure the operator
- Returns
- A list of required fields before the operator can run
Definition at line 281 of file arithmetic-operator.F90.
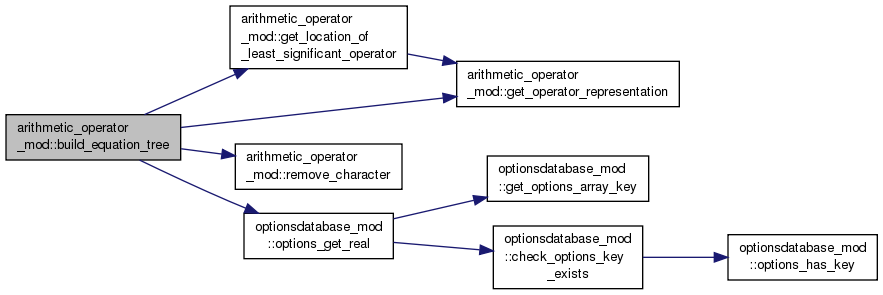
◆ build_equation_tree()
|
private |
Builds the equation tree, this searches for the least significant operator and then splits the equation based upon that. Each sub equation is then passed to recursive calls of this function which return subtrees for these aspects. Some string manipulation is done to remove braces which would otherwise be included in the terminal characters.
- Parameters
-
io_configuration Configuration of the IO server equation The equation to represent as a tree
- Returns
- The equation tree which represents the provided equation
Definition at line 182 of file arithmetic-operator.F90.

◆ execute_equation_tree()
|
private |
Executes an equation tree by doing a post order traversal of the tree. If a node is a terminal then either the variable is looked up for its value or the constant is returned. If a node is a non terminal then the operator is performed on the result value of its left and right subtrees and the value returned.
- Parameters
-
equation_tree The equation tree to traverse field_values The variable value key value pair
- Returns
- A real result from traversing this equation tree
Definition at line 132 of file arithmetic-operator.F90.

◆ finalise_arithmetic_operator()
| subroutine, public arithmetic_operator_mod::finalise_arithmetic_operator | ( | ) |
Finalises this opertor.
Definition at line 54 of file arithmetic-operator.F90.

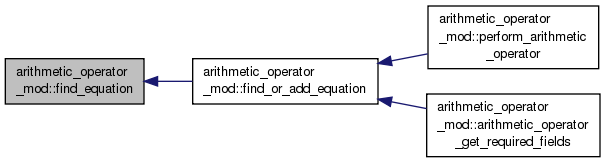
◆ find_equation()
|
private |
Finds an equation in the cache based upon its textual equation representation or returns null if none is found.
- Parameters
-
equation Textual equation that we are looking up dolock Whether to issue a read lock which accessing the collection
- Returns
- Cached entry for the equation or null if none is found
Definition at line 357 of file arithmetic-operator.F90.
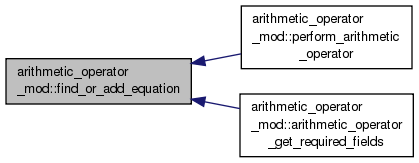
◆ find_or_add_equation()
|
private |
Locates an existing equation in the cache based upon the textual equation representation or creates a new entry and returns this one.
- Parameters
-
equation Textual equation that we are looking up
- Returns
- Cached entry for the equation
Definition at line 333 of file arithmetic-operator.F90.

◆ get_location_of_least_significant_operator()
|
private |
Given an equation this will retrieve the location of the least significant operator in that equation or 0 if no operator is found (i.e. the string is a terminal.) This takes account of parenthesis.
Definition at line 227 of file arithmetic-operator.F90.


◆ get_operator_representation()
|
private |
Given a character representation of an operator this returns the internal numeric type representation of it.
- Parameters
-
op_char The character operator representation
- Returns
- The numeric internal type of this operator or -1 if none can be found
Definition at line 260 of file arithmetic-operator.F90.

◆ get_size_of_data_being_operated_on()
|
private |
Retrieves the number of data elements that this will operate on. It will produce a log error if any variable lengths are inconsistent.
- Parameters
-
cached_equation The cached equation information field_values The variable value key value pair
- Returns
- The number of data elements being operated on
Definition at line 92 of file arithmetic-operator.F90.


◆ initialise_arithmetic_operator()
| subroutine, public arithmetic_operator_mod::initialise_arithmetic_operator | ( | ) |
Initialises this operator.
Definition at line 49 of file arithmetic-operator.F90.

◆ perform_arithmetic_operator()
| subroutine, public arithmetic_operator_mod::perform_arithmetic_operator | ( | type(io_configuration_type), intent(inout) | io_configuration, |
| type(hashmap_type), intent(inout) | field_values, | ||
| type(map_type), intent(inout) | action_attributes, | ||
| integer, intent(in) | source_monc_location, | ||
| integer, intent(in) | source_monc, | ||
| real(kind=default_precision), dimension(:), intent(inout), allocatable | operator_result_values | ||
| ) |
Executes this arithmetic operator by attempting to retrieved the cached equation (and creates one if not found.) If there is no execution tree it then parses the equation into an execution tree and stores it. The stored execution tree is then executed and the real result returned.
- Parameters
-
io_configuration Configuration of the IO server field_values The field values action_attributes Attributes associated with the running of this operator
- Returns
- The resulting value
Definition at line 66 of file arithmetic-operator.F90.
◆ process_equation_to_get_required_fields()
|
private |
Performs text processing on an equation to extract out all the required variable (fields) needed in order to run this equation and get the result. Note this ignores all values which are constants (reals or integers)
- Parameters
-
equation Text equation to extract list of required fields (variables) from
- Returns
- A list of variables needed by this equation
Definition at line 299 of file arithmetic-operator.F90.

◆ remove_character()
|
private |
Removes all occurances of a character from a string in situ by replacing it with whitespace.
- Parameters
-
raw_string The string to process and remove characters from in place c The character to search for and remove (replace by whitespace)
Definition at line 212 of file arithmetic-operator.F90.

Variable Documentation
◆ add_op
|
private |
Definition at line 25 of file arithmetic-operator.F90.
◆ div_op
|
private |
Definition at line 25 of file arithmetic-operator.F90.
◆ equation_cache
|
private |
Definition at line 40 of file arithmetic-operator.F90.
◆ equation_cache_rwlock
|
private |
Definition at line 41 of file arithmetic-operator.F90.
◆ minus_op
|
private |
Definition at line 25 of file arithmetic-operator.F90.
◆ mod_op
|
private |
A specific node in the execution tree.
Definition at line 25 of file arithmetic-operator.F90.
◆ mul_op
|
private |
Definition at line 25 of file arithmetic-operator.F90.
◆ terminal_op
|
private |
Definition at line 25 of file arithmetic-operator.F90.
 1.8.14
1.8.14