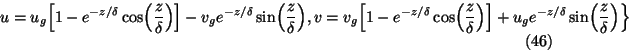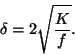3.The Atmospheric Boundary Layer
3.1 Boundary Layer Equations
Let us write the Navier-Stokes equations as
where
 is the stress tensor. In laminar flows,
is the stress tensor. In laminar flows,
 may be
expressed in terms of the viscosity. In turbulent flows, molecular viscosity
is not usually important because the Reynolds number is high. Instead,
transport by turbulent eddies is more effective. Neglecting viscosity, we
have for an incompressible flow
may be
expressed in terms of the viscosity. In turbulent flows, molecular viscosity
is not usually important because the Reynolds number is high. Instead,
transport by turbulent eddies is more effective. Neglecting viscosity, we
have for an incompressible flow
As for the case of turbulent transport of a tracer, we put
Substituting Eq. (31) into (29)-(30) and averaging
Close to the surface, variations in the vertical dominate horizontal
variations so that we can neglect  and
and 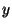 derivatives. Furthermore, the
mean flow is almost horizontal so that
derivatives. Furthermore, the
mean flow is almost horizontal so that 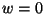 . Therefore
. Therefore
It turns out that on the scale of the whole boundary layer, we cannot
neglect the effect of the rotation of the Earth. This effect is included
by working in a frame of reference fixed relative to the surface of the
Earth in the region of interest (this is of course a rotating, or
non-inertial frame of reference). The frame of reference is rotating with
angular speed
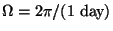 . In the rotating frame of
reference the equations of motion become
. In the rotating frame of
reference the equations of motion become
The extra terms which have been introduced are called the Coriolis
force. 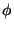 is the latitude.
is the latitude.
As for the case of scalar transport, we assume that
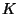 is called the eddy viscosity. We often write
is called the eddy viscosity. We often write
where
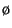 is the turbulent stress.
is the turbulent stress.
3.2 Constant Stress Layer --- The Surface Layer
There is a thin region close to the surface where the stress
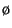 does not vary much from its surface value and so it can be assumed to be
constant. This is called the surface layer. In the surface layer
does not vary much from its surface value and so it can be assumed to be
constant. This is called the surface layer. In the surface layer
Let the wind speed  be given by
be given by
and let
where 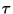 is the magnitude of the surface stress. Because the direction
of the stress does not vary with height in the surface layer it follows
from Eq. (36) that
is the magnitude of the surface stress. Because the direction
of the stress does not vary with height in the surface layer it follows
from Eq. (36) that
We usually write the constant stress 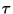 as
as
where 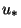 is a quantity called the friction velocity. We can use
arguments from dimensional analysis to evaluate the eddy viscosity
is a quantity called the friction velocity. We can use
arguments from dimensional analysis to evaluate the eddy viscosity 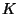 . It
turns out that the only scales available to us are
. It
turns out that the only scales available to us are 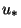 and the height
and the height 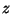 itself. In terms of these we have
itself. In terms of these we have
Physically this indicates that at greater heights, larger turbulent eddies
are acting to transport momentum. We put
where 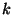 is a constant called von Kármán's constant. It is usually taken
as
is a constant called von Kármán's constant. It is usually taken
as 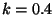 . From Eq. (37), (38) and (39)
. From Eq. (37), (38) and (39)
Solving this for  we get
we get
where 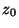 is a constant. Note that as
is a constant. Note that as 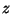 decreases towards zero,
decreases towards zero,  goes
to zero at
goes
to zero at 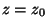 .
. 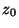 is called the roughness length and it is a
measure of the size of the so-called roughness elements making up the surface.
These roughness elements could be grains of sand, blades of grass, bushes,
trees, etc.
is called the roughness length and it is a
measure of the size of the so-called roughness elements making up the surface.
These roughness elements could be grains of sand, blades of grass, bushes,
trees, etc.
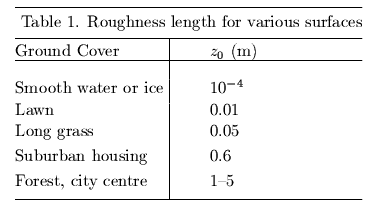
Eq. (41) usually applies up to a few tens of metres from the ground.
3.3 Effect of Stability
Under some circumstances (particularly at night when there is no cloud)
the surface cools by radiation into space and the layer of air close to the
surface becomes cold and dense.
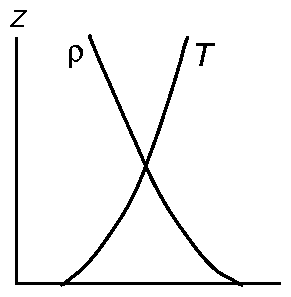
Fig. 5. Temperature and density profiles close to the
surface on a clear night. The air close to the surface is stably
stratified.
This stable stratification inhibits vertical eddy motion. This can
be thought of as reducing the size of the turbulent eddies so that
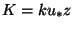 no longer applies. Another way to think about the problem is that
there is another length scale, in addition to
no longer applies. Another way to think about the problem is that
there is another length scale, in addition to 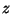 , introduced into the
problem. This is
, introduced into the
problem. This is
where 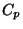 is the specific heat capacity at constant pressure,
is the specific heat capacity at constant pressure, 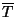 is
an average temperature (absolute) and
is
an average temperature (absolute) and 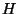 is the surface heat flux. For
surface cooling,
is the surface heat flux. For
surface cooling, 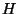 is negative and so
is negative and so 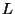 is positive.
is positive. 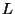 is called the
Monin-Obukhov length. It is found experimentally that for stable stratification
a reasonable approximation is
is called the
Monin-Obukhov length. It is found experimentally that for stable stratification
a reasonable approximation is
so that
where 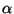 is a constant. Typically,
is a constant. Typically,
 . The solution of
Eq. (43) is
. The solution of
Eq. (43) is
3.4 The Ekman Layer
On a scale deeper than the surface layer, we can, to a crude approximation,
take
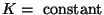 . For neutral stratification,
. For neutral stratification,  m
m s
s .
If the flow is steady, Eq. (32)-(34) become
.
If the flow is steady, Eq. (32)-(34) become
In the boundary layer we can assume that
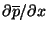 and
and
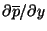 are independent of height and are given by
are independent of height and are given by
where 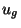 and
and 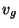 are called the geostrophic wind components. For
our purposes, we can take them to be the wind above the boundary layer.
Let
are called the geostrophic wind components. For
our purposes, we can take them to be the wind above the boundary layer.
Let
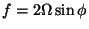 -- the Coriolis parameter. Then
-- the Coriolis parameter. Then
These are the Ekman equations. The solutions are
where
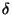 is a measure of the thickness of the atmospheric boundary layer.
In mid-latitudes,
is a measure of the thickness of the atmospheric boundary layer.
In mid-latitudes,
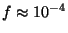 s
s and we find that
and we find that
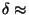 500 m.
500 m.
The Ekman solution (46) shows that the wind direction varies within the
boundary layer and that the wind vectors form a spiral with increasing height
(see Fig. 7).
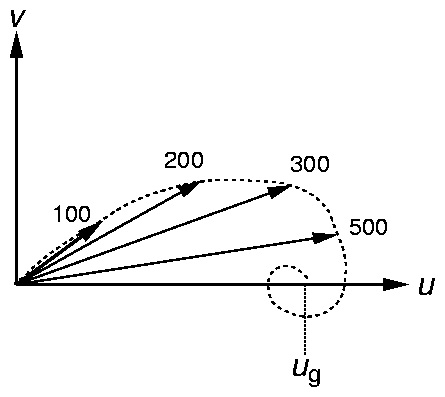
Fig. 7. Wind vectors in the Ekman boundary layer.
The heights of the wind vectors are shown in metres.
back to syllabus

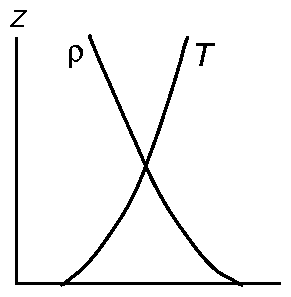
![]() no longer applies. Another way to think about the problem is that
there is another length scale, in addition to
no longer applies. Another way to think about the problem is that
there is another length scale, in addition to ![]() , introduced into the
problem. This is
, introduced into the
problem. This is