2 Transport Processes
2.1 Diffusion Without Shear
(i) Instantaneous plane source in 3-dimensions
Suppose that the initial distribution of 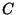 is dependent only on
is dependent only on  and
and
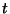 and that
and that  ,
,  and
and 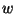 are constant. Then Eq. (14) reduces to
are constant. Then Eq. (14) reduces to
We now transform to a frame of reference moving with the flow speed  :
:
Then Eq. (15) becomes
Suppose that
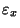 is constant. Then the solution to Eq. (16) is
is constant. Then the solution to Eq. (16) is
It can be shown that
The solution (17) can
be interpreted as an instantaneous release of an amount  kgm
kgm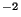 of
pollutant at
of
pollutant at 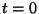 in the plane
in the plane 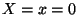 . Eq. (17) is the Gaussian ``puff''
solution because it describes the release of a small ``puff'' of pollutant.
. Eq. (17) is the Gaussian ``puff''
solution because it describes the release of a small ``puff'' of pollutant.
An important quantity is the mean square distance 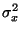 which the
pollutant has spread from
which the
pollutant has spread from 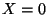 . This is given by
. This is given by
Therefore
The pollutant therefore spreads at a rate proportional to 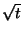 .
.
(ii) Instantaneous line source in 3-dimensions
In this case we assume that  so that the equation for
so that the equation for
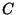 is
is
As in the previous case we make the transformation 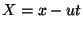 and also
let
and also
let 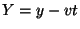 . Then
. Then
The solution is
It can be shown that
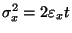 and
and
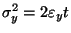 . Hence
. Hence
(iii) Instantaneous point source in 3-dimensions
This is the most general and practical case where 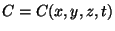 .
The equation for
.
The equation for 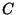 is
is
We
could put 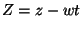 in line with the cases of plane and line sources but
it is difficult to think of real cases where there is a mean vertical velocity
in line with the cases of plane and line sources but
it is difficult to think of real cases where there is a mean vertical velocity
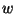 so we keep
so we keep 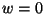 . The transsformed equation for
. The transsformed equation for  is then
is then
The solution is
In this case
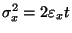 ,
,
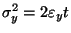 and
and
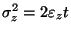 so that
so that
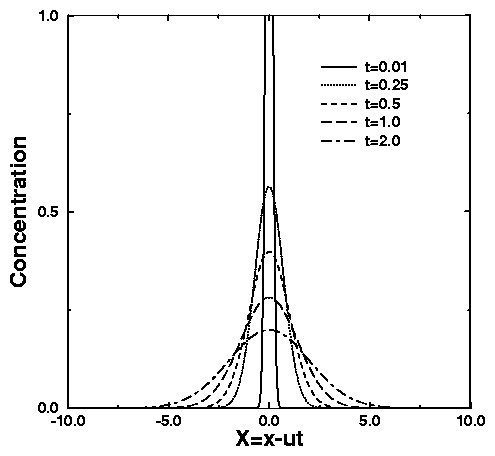
Fig. 2. Concentration distributions at various times
after pollutant release for the diffusion of an instantaneous plane source
(Eq. (20)).
2.2 Advection Without Diffusion in a Shear Flow
Suppose that we have a uni-directional shear flow:
and suppose that we are interested in the flow between  and
and  .
.

Fig. 3. Shear flow 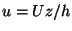 .
.
If we neglect diffusion, then the equation for 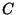 is
is
If we again put 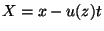 Eq. (26) becomes
Eq. (26) becomes
and so 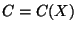 , i.e. the concentration is independent of time moving with
the local flow
, i.e. the concentration is independent of time moving with
the local flow 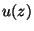 . Consider as in the previous section the case of an
instantaneous plane source at
. Consider as in the previous section the case of an
instantaneous plane source at 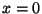 ,
, 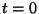 . Then at
. Then at 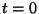
This must be the solution for all time, because
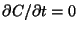 .
Therefore
.
Therefore
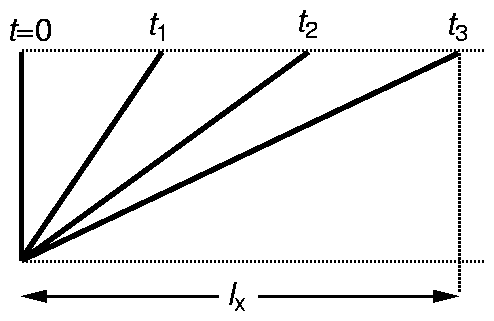
Fig. 4. A line (or plane in 3-D) of pollutant
initially lying on 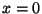 is stretched and rotated by a shear flow
is stretched and rotated by a shear flow 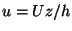 .
At time
.
At time 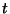 the
the  extent of the line of pollutant is denoted by
extent of the line of pollutant is denoted by 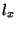 .
.
Consider the horizontal extent 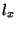 of the pollutant. At time
of the pollutant. At time 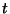 it is
clearly
it is
clearly
We can see that the pollutant spreads out at a rate proportional to 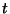 . This
contrasts with the rate proportional to
. This
contrasts with the rate proportional to 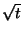 for diffusion, so it would
appear that advection is always more important than diffusion, except perhaps
for a short time after release. However, we shall see in the next section
that this is not the case.
for diffusion, so it would
appear that advection is always more important than diffusion, except perhaps
for a short time after release. However, we shall see in the next section
that this is not the case.
2.3 Advection and Diffusion in a Shear Flow
When advection and diffusion occur simultaneously, the stretching of
regions of high concentration, as occurs for pure advection, is less
effective because transverse diffusion of the high concentration region is
enhanced by the stretching caused by the shear. This is shown schematically
in Fig. 5.
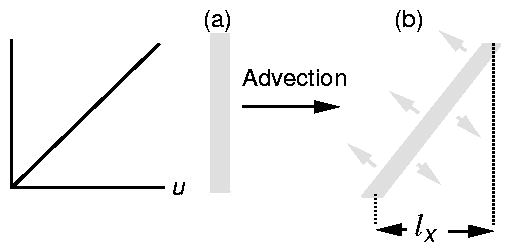
Fig. 5. An initial slab (a) of pollutant is rotated
and stretched by shear (b), leading to enhanced diffusion in the transverse
direction (c). The spreading of the line of maximum concentration is clearly
reduced by the diffusion.
The processes described here are known as Taylor's mechanism.
back to syllabus
![]() is dependent only on
is dependent only on ![]() and
and
![]() and that
and that ![]() ,
, ![]() and
and ![]() are constant. Then Eq. (14) reduces to
are constant. Then Eq. (14) reduces to
![]() which the
pollutant has spread from
which the
pollutant has spread from ![]() . This is given by
. This is given by
![]() so that the equation for
so that the equation for
![]() is
is
![]() .
The equation for
.
The equation for ![]() is
is


![]() .
.
![]() is
is
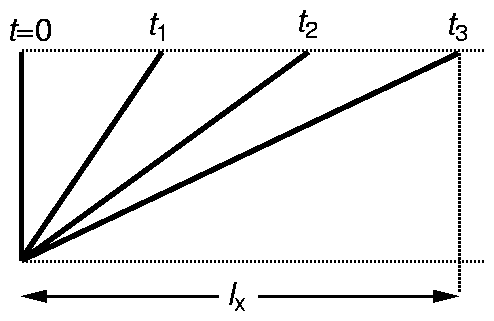
![]() is stretched and rotated by a shear flow
is stretched and rotated by a shear flow ![]() .
At time
.
At time ![]() the
the ![]() extent of the line of pollutant is denoted by
extent of the line of pollutant is denoted by ![]() .
.
![]() of the pollutant. At time
of the pollutant. At time ![]() it is
clearly
it is
clearly
